Tìm số lớn thứ 2 trong mảng 1 chiều
Tìm số lớn thứ 2 trong mảng là một bài toán phổ biến trong lập trình, thường xuất hiện trong các cuộc phỏng vấn và các kỳ thi lập trình. Bài viết này sẽ hướng dẫn bạn cách giải quyết bài toán này một cách hiệu quả nhất.
Giới thiệu bài toán
Bài toán tìm số lớn thứ 2 trong mảng yêu cầu chúng ta:
- Cho một mảng số nguyên
- Tìm phần tử có giá trị lớn thứ 2 trong mảng
- Xử lý các trường hợp đặc biệt như mảng có phần tử trùng nhau
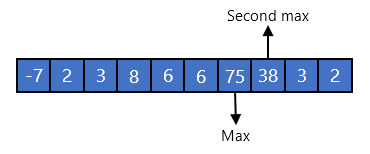
Phân tích bài toán
Khi giải bài toán này, bạn nên chú ý đến các trường hợp đặc biệt sau đây:
- Mảng có ít hơn 2 phần tử
- Mảng có các phần tử giống nhau
- Mảng không có số lớn thứ 2 (tất cả phần tử bằng nhau)
Trước khi đi vào các phương pháp giải quyết, bạn hãy dành một chút thời gian để tự mình suy nghĩ về bài toán này. Việc tự tìm ra lời giải sẽ giúp bạn phát triển tư duy giải quyết vấn đề và ghi nhớ kiến thức tốt hơn. Sau khi đã có ý tưởng của riêng mình, bạn có thể tham khảo các phương pháp được trình bày dưới đây để hoàn thiện giải pháp của mình.
Thực hành nhiều bài tập hơn tại https://luyencode.net
Các phương pháp giải
Chúng ta sẽ đi từ phương án dễ triển khai (ít tối ưu) đến phương án đòi hỏi suy luận nhiều hơn (tối ưu) nhé.
Phương pháp sắp xếp
Ý tưởng:
- Sắp xếp mảng theo thứ tự giảm dần
- Duyệt mảng để tìm phần tử khác với số lớn nhất đầu tiên
- Độ phức tạp: O(nlogn)
Giải thích chi tiết:
- Kiểm tra điều kiện đầu vào:
- Nếu mảng có ít hơn 2 phần tử, trả về -1
- Sắp xếp mảng:
- Sử dụng hàm sort với greater() để sắp xếp theo thứ tự giảm dần
- Sau khi sắp xếp, phần tử lớn nhất sẽ ở vị trí đầu tiên (arr[0])
- Tìm số lớn thứ 2:
- Duyệt mảng từ vị trí thứ 2
- Trả về phần tử đầu tiên khác với số lớn nhất
- Nếu không tìm thấy, trả về -1
Code mẫu
#include <iostream>
#include <algorithm>
using namespace std;
int findSecondMaxSort(int arr[], int n) {
// Check input condition
if (n < 2) {
return -1; // Array doesn't have enough elements
}
// Sort array in descending order
sort(arr, arr + n, greater<int>());
// Find first element different from max
for (int i = 1; i < n; i++) {
if (arr[i] != arr[0]) {
return arr[i];
}
}
return -1; // No second largest element found
}
int main() {
int arr[] = {12, 35, 1, 10, 34, 1};
int n = sizeof(arr)/sizeof(arr[0]);
int second = findSecondMaxSort(arr, n);
if (second != -1) {
cout << "Second largest element is: " << second << endl;
} else {
cout << "No second largest element found" << endl;
}
return 0;
}import java.util.Arrays;
import java.util.Collections;
public class SecondMaxFinder {
public static int findSecondMaxSort(Integer[] arr, int n) {
// Check input condition
if (n < 2) {
return -1; // Array doesn't have enough elements
}
// Sort array in descending order
Arrays.sort(arr, Collections.reverseOrder());
// Find first element different from max
for (int i = 1; i < n; i++) {
if (arr[i] != arr[0]) {
return arr[i];
}
}
return -1; // No second largest element found
}
public static void main(String[] args) {
Integer[] arr = {12, 35, 1, 10, 34, 1};
int n = arr.length;
int second = findSecondMaxSort(arr, n);
if (second != -1) {
System.out.println("Second largest element is: " + second);
} else {
System.out.println("No second largest element found");
}
}
}def find_second_max_sort(arr, n):
# Check input condition
if n < 2:
return -1 # Array doesn't have enough elements
# Sort array in descending order
arr.sort(reverse=True)
# Find first element different from max
for i in range(1, n):
if arr[i] != arr[0]:
return arr[i]
return -1 # No second largest element found
if __name__ == "__main__":
arr = [12, 35, 1, 10, 34, 1]
n = len(arr)
second = find_second_max_sort(arr, n)
if second != -1:
print("Second largest element is:", second)
else:
print("No second largest element found")Phương pháp duyệt 2 lần
Ý tưởng
- Lần 1: Tìm số lớn nhất
- Lần 2: Tìm số lớn nhất trong các số nhỏ hơn max
- Độ phức tạp: O(n)
Giải thích chi tiết
- Kiểm tra điều kiện đầu vào:
- Nếu mảng có ít hơn 2 phần tử, trả về -1
- Lần duyệt thứ nhất:
- Tìm số lớn nhất trong mảng (max)
- Lưu giá trị này để so sánh ở lần duyệt thứ hai
- Lần duyệt thứ hai:
- Tìm số lớn nhất trong các số nhỏ hơn max
- Sử dụng second_max để lưu kết quả
- Nếu không tìm thấy (second_max = INT_MIN), trả về -1
Code mẫu
#include <iostream>
#include <climits>
using namespace std;
int findSecondMaxTwoPass(int arr[], int n) {
// Check input condition
if (n < 2) {
return -1; // Array doesn't have enough elements
}
// First pass: find maximum element
int max = arr[0];
for (int i = 1; i < n; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
// Second pass: find second maximum
int second_max = INT_MIN;
for (int i = 0; i < n; i++) {
if (arr[i] != max && arr[i] > second_max) {
second_max = arr[i];
}
}
// Check if second maximum exists
if (second_max == INT_MIN) {
return -1;
}
return second_max;
}
int main() {
int arr[] = {12, 35, 1, 10, 34, 1};
int n = sizeof(arr)/sizeof(arr[0]);
int second = findSecondMaxTwoPass(arr, n);
if (second != -1) {
cout << "Second largest element is: " << second << endl;
} else {
cout << "No second largest element found" << endl;
}
return 0;
}#include <iostream>
#include <climits>
using namespace std;
int findSecondMaxTwoPass(int arr[], int n) {
// Check input condition
if (n < 2) {
return -1; // Array doesn't have enough elements
}
// First pass: find maximum element
int max = arr[0];
for (int i = 1; i < n; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
// Second pass: find second maximum
int second_max = INT_MIN;
for (int i = 0; i < n; i++) {
if (arr[i] != max && arr[i] > second_max) {
second_max = arr[i];
}
}
// Check if second maximum exists
if (second_max == INT_MIN) {
return -1;
}
return second_max;
}
int main() {
int arr[] = {12, 35, 1, 10, 34, 1};
int n = sizeof(arr)/sizeof(arr[0]);
int second = findSecondMaxTwoPass(arr, n);
if (second != -1) {
cout << "Second largest element is: " << second << endl;
} else {
cout << "No second largest element found" << endl;
}
return 0;
}import sys
def findSecondMaxTwoPass(arr, n):
# Check input condition
if n < 2:
return -1 # Array doesn't have enough elements
# First pass: find maximum element
max_val = arr[0]
for i in range(1, n):
if arr[i] > max_val:
max_val = arr[i]
# Second pass: find second maximum
second_max = -sys.maxsize - 1 # Equivalent to INT_MIN in C++
for i in range(n):
if arr[i] != max_val and arr[i] > second_max:
second_max = arr[i]
# Check if second maximum exists
if second_max == -sys.maxsize - 1:
return -1
return second_max
if __name__ == "__main__":
arr = [12, 35, 1, 10, 34, 1]
n = len(arr)
second = findSecondMaxTwoPass(arr, n)
if second != -1:
print("Second largest element is:", second)
else:
print("No second largest element found")Phương Pháp Duyệt 1 Lần (Tối Ưu)
Ý tưởng
- Sử dụng 2 biến để lưu số lớn nhất và lớn thứ 2
- Cập nhật trong quá trình duyệt mảng
- Độ phức tạp: O(n)
Giải thích chi tiết
- Kiểm tra điều kiện đầu vào:
- Nếu mảng có ít hơn 2 phần tử, trả về -1
- Khởi tạo biến:
max: lưu giá trị lớn nhấtsecond_max: lưu giá trị lớn thứ 2- Ban đầu cả hai đều được gán giá trị INT_MIN
- Duyệt mảng một lần:
- Nếu phần tử hiện tại lớn hơn max:
- Cập nhật second_max = max cũ
- Cập nhật max = giá trị mới
- Nếu phần tử hiện tại lớn hơn second_max và nhỏ hơn max:
- Cập nhật second_max = giá trị hiện tại
- Nếu phần tử hiện tại lớn hơn max:
- Kiểm tra kết quả:
- Nếu second_max vẫn là INT_MIN, không tìm thấy số lớn thứ 2
- Ngược lại, trả về giá trị second_max
Code mẫu
#include <iostream>
#include <climits>
using namespace std;
int findSecondMax(int arr[], int n) {
// Kiểm tra điều kiện đầu vào
if (n < 2) {
return -1; // Mảng không đủ phần tử
}
// Khởi tạo max và second_max
int max = INT_MIN;
int second_max = INT_MIN;
// Duyệt mảng một lần
for (int i = 0; i < n; i++) {
// Nếu tìm thấy phần tử lớn hơn max
if (arr[i] > max) {
second_max = max; // Cập nhật second_max
max = arr[i]; // Cập nhật max
}
// Nếu phần tử lớn hơn second_max và khác max
else if (arr[i] > second_max && arr[i] < max) {
second_max = arr[i];
}
}
// Kiểm tra nếu không tìm thấy số lớn thứ 2
if (second_max == INT_MIN) {
return -1;
}
return second_max;
}
int main() {
// Ví dụ sử dụng
int arr[] = {12, 35, 1, 10, 34, 1};
int n = sizeof(arr)/sizeof(arr[0]);
int second = findSecondMax(arr, n);
if (second != -1) {
cout << "Second largest element is: " << second << endl;
} else {
cout << "No second largest element found" << endl;
}
return 0;
}public class SecondMax {
public static int findSecondMax(int[] arr, int n) {
// Kiểm tra điều kiện đầu vào
if (n < 2) {
return -1; // Mảng không đủ phần tử
}
// Khởi tạo max và second_max
int max = Integer.MIN_VALUE;
int second_max = Integer.MIN_VALUE;
// Duyệt mảng một lần
for (int i = 0; i < n; i++) {
// Nếu tìm thấy phần tử lớn hơn max
if (arr[i] > max) {
second_max = max; // Cập nhật second_max
max = arr[i]; // Cập nhật max
}
// Nếu phần tử lớn hơn second_max và khác max
else if (arr[i] > second_max && arr[i] < max) {
second_max = arr[i];
}
}
// Kiểm tra nếu không tìm thấy số lớn thứ 2
if (second_max == Integer.MIN_VALUE) {
return -1;
}
return second_max;
}
public static void main(String[] args) {
// Ví dụ sử dụng
int[] arr = {12, 35, 1, 10, 34, 1};
int n = arr.length;
int second = findSecondMax(arr, n);
if (second != -1) {
System.out.println("Second largest element is: " + second);
} else {
System.out.println("No second largest element found");
}
}
}import sys
def findSecondMax(arr, n):
# Kiểm tra điều kiện đầu vào
if n < 2:
return -1 # Mảng không đủ phần tử
# Khởi tạo max và second_max
max_val = -sys.maxsize - 1
second_max = -sys.maxsize - 1
# Duyệt mảng một lần
for i in range(n):
# Nếu tìm thấy phần tử lớn hơn max
if arr[i] > max_val:
second_max = max_val # Cập nhật second_max
max_val = arr[i] # Cập nhật max
# Nếu phần tử lớn hơn second_max và khác max
elif arr[i] > second_max and arr[i] < max_val:
second_max = arr[i]
# Kiểm tra nếu không tìm thấy số lớn thứ 2
if second_max == -sys.maxsize - 1:
return -1
return second_max
# Ví dụ sử dụng
if __name__ == "__main__":
arr = [12, 35, 1, 10, 34, 1]
n = len(arr)
second = findSecondMax(arr, n)
if second != -1:
print("Second largest element is:", second)
else:
print("No second largest element found")Lời kết
Tìm số lớn thứ 2 trong mảng là một bài toán tuy đơn giản nhưng đòi hỏi sự tỉ mỉ trong việc xử lý các trường hợp đặc biệt. Thuật toán one-pass được trình bày ở trên là giải pháp tối ưu nhất với độ phức tạp O(n). Hy vọng bài viết này giúp bạn hiểu rõ hơn về bài toán và các cách giải quyết hiệu quả.
Tham khảo thêm: Chinh phục 1000 bài tập lập trình (có lời giải).
Tài liệu tham khảo
- Introduction to Algorithms – Thomas H. Cormen.
- Data Structures and Algorithm Analysis – Mark Allen Weiss.






