Tìm kiếm nhị phân – Giải thuật kinh điển cần biết
Thuật toán tìm kiếm nhị phân là một trong những thuật toán tìm kiếm hiệu quả nhất trong khoa học máy tính. Với độ phức tạp O(log n), thuật toán này đặc biệt phù hợp với các tập dữ liệu lớn đã được sắp xếp. Bằng cách liên tục chia đôi phạm vi tìm kiếm theo nguyên lý chia để trị, thuật toán có thể nhanh chóng thu hẹp khu vực cần xét để tìm ra kết quả. Thuật toán này có thể được triển khai linh hoạt thông qua hai cách tiếp cận: sử dụng vòng lặp hoặc đệ quy. Trong thực tế, tìm kiếm nhị phân được ứng dụng rộng rãi từ việc tìm kiếm trong mảng đơn giản đến các bài toán tối ưu phức tạp, chứng tỏ tính ứng dụng cao của thuật toán này.
Trong bài viết này, chúng ta sẽ cùng khám phá thuật toán tìm kiếm nhị phân – một trong những thuật toán cơ bản nhưng vô cùng mạnh mẽ mà mọi lập trình viên đều nên nắm vững. Đây không chỉ là kiến thức nền tảng trong học tập mà còn là công cụ hữu ích trong công việc thực tế.
Thuật toán tìm kiếm nhị phân là gì?
Thuật toán tìm kiếm nhị phân là một phương pháp tìm kiếm hiệu quả áp dụng cho **dữ liệu đã được sắp xếp**. Thay vì kiểm tra từng phần tử một như tìm kiếm tuyến tính, tìm kiếm nhị phân liên tục chia đôi phạm vi tìm kiếm, giúp loại bỏ một nửa số phần tử cần xét sau mỗi bước so sánh.
Điều này giúp giảm độ phức tạp thời gian từ O(n) của tìm kiếm tuyến tính xuống còn O(log n) – một sự cải thiện đáng kể, đặc biệt khi làm việc với tập dữ liệu lớn.
Nguyên lý hoạt động
Thuật toán tìm kiếm nhị phân hoạt động theo các bước sau:
- Xác định phạm vi tìm kiếm ban đầu (toàn bộ mảng)
- Tìm phần tử ở giữa của phạm vi hiện tại
- So sánh phần tử giữa với giá trị cần tìm:
- Nếu bằng nhau: Tìm thấy kết quả
- Nếu phần tử giữa lớn hơn: Tiếp tục tìm ở nửa bên trái
- Nếu phần tử giữa nhỏ hơn: Tiếp tục tìm ở nửa bên phải
- Lặp lại bước 2-3 cho đến khi tìm thấy hoặc phạm vi tìm kiếm trống
Mã giả (Pseudocode)
Trước khi đi vào mã nguồn C++, hãy xem mã giả của thuật toán tìm kiếm nhị phân:
FUNCTION BinarySearch(arr, target)
left = 0
right = length(arr) - 1
WHILE left <= right
mid = left + (right - left) / 2
IF arr[mid] = target THEN
RETURN mid
ELSE IF arr[mid] > target THEN
right = mid - 1
ELSE
left = mid + 1
END IF
END WHILE
RETURN -1 // Không tìm thấy
END FUNCTIONMinh hoạ trực quan
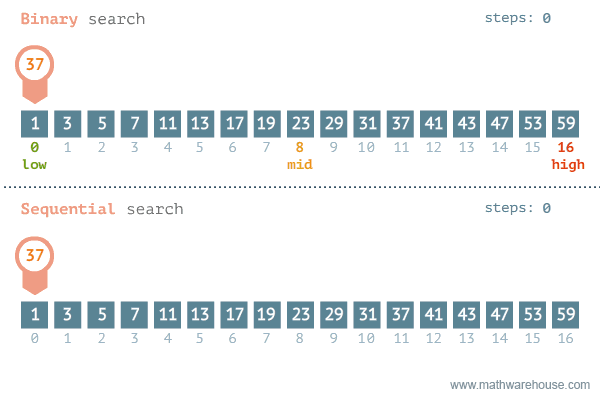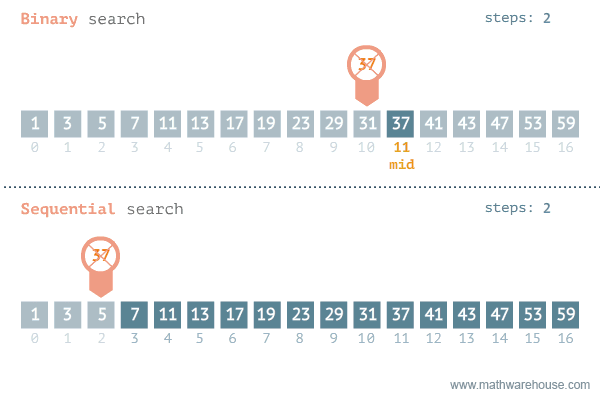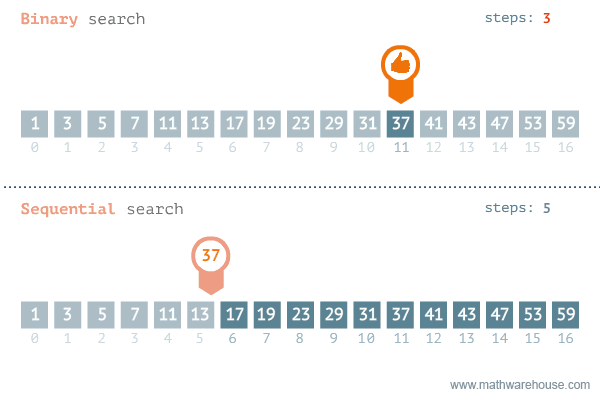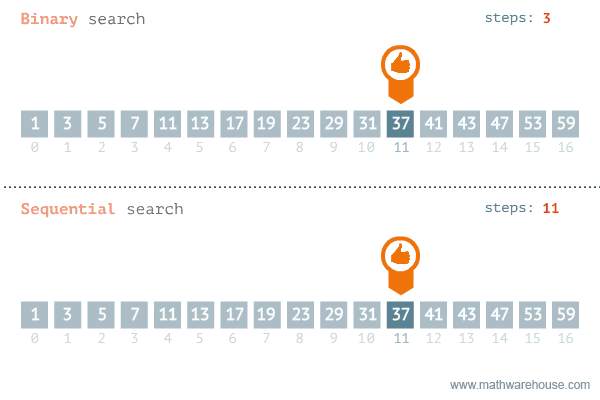
So sánh tìm kiếm tuyến tính và tìm kiếm nhị phân
| Tiêu chí | Tìm kiếm tuyến tính | Tìm kiếm nhị phân |
|---|---|---|
| Cách thức hoạt động | Kiểm tra từng phần tử một theo thứ tự | Thu hẹp phạm vi tìm kiếm bằng cách chia đôi |
| Số phần tử cần kiểm tra | Tối đa n phần tử | Tối đa log(n) phần tử |
| Hiệu quả | Kém hiệu quả với dữ liệu lớn | Hiệu quả cao với dữ liệu lớn |
| Yêu cầu | Không yêu cầu dữ liệu sắp xếp | Yêu cầu dữ liệu đã sắp xếp |
Cài đặt thuật toán tìm kiếm nhị phân
Phiên bản sử dụng vòng lặp
#include <iostream>
#include <vector>
using namespace std;
// Hàm tìm kiếm nhị phân sử dụng vòng lặp
int binarySearch(vector<int>& arr, int target) {
int left = 0;
int right = arr.size() - 1;
while (left <= right) {
// Tính chỉ số giữa, tránh tràn số với cách tính này
int mid = left + (right - left) / 2;
// Kiểm tra nếu phần tử ở giữa là giá trị cần tìm
if (arr[mid] == target) {
return mid; // Trả về vị trí tìm thấy
}
// Nếu giá trị cần tìm nhỏ hơn phần tử giữa, tìm bên trái
if (arr[mid] > target) {
right = mid - 1;
}
// Nếu giá trị cần tìm lớn hơn phần tử giữa, tìm bên phải
else {
left = mid + 1;
}
}
// Trả về -1 nếu không tìm thấy
return -1;
}
int main() {
vector<int> arr = {1, 3, 5, 7, 9, 11, 13, 15, 17};
int target;
cout << "Enter the number to search: ";
cin >> target;
int result = binarySearch(arr, target);
if (result != -1) {
cout << "Element found at index " << result << endl;
} else {
cout << "Element not found in the array" << endl;
}
return 0;
}Phiên bản sử dụng đệ quy
#include <iostream>
#include <vector>
using namespace std;
// Hàm tìm kiếm nhị phân sử dụng đệ quy
int binarySearchRecursive(vector<int>& arr, int left, int right, int target) {
// Điều kiện dừng: không còn phần tử để tìm
if (left > right) {
return -1;
}
// Tính chỉ số giữa
int mid = left + (right - left) / 2;
// Nếu phần tử ở giữa là giá trị cần tìm
if (arr[mid] == target) {
return mid;
}
// Nếu giá trị cần tìm nhỏ hơn phần tử giữa, tìm bên trái
if (arr[mid] > target) {
return binarySearchRecursive(arr, left, mid - 1, target);
}
// Nếu giá trị cần tìm lớn hơn phần tử giữa, tìm bên phải
return binarySearchRecursive(arr, mid + 1, right, target);
}
// Hàm wrapper để gọi hàm đệ quy
int binarySearch(vector<int>& arr, int target) {
return binarySearchRecursive(arr, 0, arr.size() - 1, target);
}
int main() {
vector<int> arr = {1, 3, 5, 7, 9, 11, 13, 15, 17};
int target;
cout << "Enter the number to search: ";
cin >> target;
int result = binarySearch(arr, target);
if (result != -1) {
cout << "Element found at index " << result << endl;
} else {
cout << "Element not found in the array" << endl;
}
return 0;
}Tham khảo thêm: Hoán vị 2 số trong C/C++ (nhiều phương án).
Phân tích thuật toán tìm kiếm nhị phân
Độ phức tạp thời gian
Độ phức tạp thời gian của thuật toán tìm kiếm nhị phân là O(log n), trong đó n là số phần tử trong mảng. Điều này có nghĩa là ngay cả khi kích thước mảng tăng lên gấp đôi, số bước tìm kiếm chỉ tăng thêm 1.
Để hiểu rõ hơn, hãy xem bảng so sánh sau (trong trường hợp xấu/tệ nhất):
| Kích thước mảng | Tìm kiếm tuyến tính (O(n)) | Tìm kiếm nhị phân (O(log n)) |
|---|---|---|
| 10 | 10 bước (tệ nhất) | 4 bước (tệ nhất) |
| 100 | 100 bước (tệ nhất) | 7 bước (tệ nhất) |
| 1,000 | 1,000 bước (tệ nhất) | 10 bước (tệ nhất) |
| 1,000,000 | 1,000,000 bước (tệ nhất) | 20 bước (tệ nhất) |
| 1,000,000,000 | 1,000,000,000 bước (tệ nhất) | 30 bước (tệ nhất) |
Như bạn có thể thấy, với một tỷ phần tử, tìm kiếm nhị phân chỉ cần tối đa 30 bước so sánh!
Độ phức tạp không gian
- Phiên bản vòng lặp: O(1) – chỉ sử dụng một số biến cố định
- Phiên bản đệ quy: O(log n) – do ngăn xếp cuộc gọi đệ quy
Các biến thể và ứng dụng nâng cao
Tìm vị trí chèn
Một biến thể phổ biến của tìm kiếm nhị phân là tìm vị trí để chèn một phần tử mới vào mảng đã sắp xếp:
// Tìm vị trí chèn để giữ mảng vẫn được sắp xếp
int findInsertPosition(vector<int>& arr, int target) {
int left = 0;
int right = arr.size() - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
return mid; // Vị trí đã tồn tại phần tử giống target
}
if (arr[mid] > target) {
right = mid - 1;
} else {
left = mid + 1;
}
}
// Trả về vị trí cần chèn
return left;
}Ví dụ cụ thể:
Mảng: [1, 3, 5, 7, 9]
Giá trị cần chèn: 4
Các bước thực hiện:
1. left = 0, right = 4, mid = 2, arr[mid] = 5
4 < 5, thu hẹp phạm vi bên trái: right = 1
2. left = 0, right = 1, mid = 0, arr[mid] = 1
4 > 1, thu hẹp phạm vi bên phải: left = 1
3. left = 1, right = 1, mid = 1, arr[mid] = 3
4 > 3, thu hẹp phạm vi bên phải: left = 2
4. left = 2, right = 1 (left > right), thoát vòng lặp
Kết quả: 2 (vị trí giữa 3 và 5)
Tham khảo thêm: LRU Cache là gì? Cách hoạt động và triển khai chi tiết
Tìm phần tử đầu tiên và cuối cùng
Khi mảng có các phần tử trùng lặp, đôi khi chúng ta cần tìm vị trí đầu tiên hoặc cuối cùng của một giá trị:
// Tìm vị trí đầu tiên của target trong mảng
int findFirstOccurrence(vector<int>& arr, int target) {
int left = 0;
int right = arr.size() - 1;
int result = -1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
result = mid; // Lưu kết quả hiện tại
right = mid - 1; // Tiếp tục tìm bên trái
} else if (arr[mid] > target) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return result;
}
// Tìm vị trí cuối cùng của target trong mảng
int findLastOccurrence(vector<int>& arr, int target) {
int left = 0;
int right = arr.size() - 1;
int result = -1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
result = mid; // Lưu kết quả hiện tại
left = mid + 1; // Tiếp tục tìm bên phải
} else if (arr[mid] > target) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return result;
}Ví dụ cụ thể:
Mảng: [1, 2, 2, 2, 3, 4, 5]
Giá trị cần tìm: 2
Tìm vị trí đầu tiên:
1. left = 0, right = 6, mid = 3, arr[mid] = 2
Đã tìm thấy, lưu result = 3, tiếp tục tìm bên trái: right = 2
2. left = 0, right = 2, mid = 1, arr[mid] = 2
Đã tìm thấy, lưu result = 1, tiếp tục tìm bên trái: right = 0
3. left = 0, right = 0, mid = 0, arr[mid] = 1
1 != 2, thu hẹp phạm vi bên phải: left = 1
4. left = 1, right = 0 (left > right), thoát vòng lặp
Kết quả: Vị trí đầu tiên là 1
Tìm vị trí cuối cùng:
1. left = 0, right = 6, mid = 3, arr[mid] = 2
Đã tìm thấy, lưu result = 3, tiếp tục tìm bên phải: left = 4
2. left = 4, right = 6, mid = 5, arr[mid] = 4
4 > 2, thu hẹp phạm vi bên trái: right = 4
3. left = 4, right = 4, mid = 4, arr[mid] = 3
3 > 2, thu hẹp phạm vi bên trái: right = 3
4. left = 4, right = 3 (left > right), thoát vòng lặp
Kết quả: Vị trí cuối cùng là 3
Ứng dụng thực tế
Thuật toán tìm kiếm nhị phân có nhiều ứng dụng thực tế:
1. Tìm kiếm trong cơ sở dữ liệu
Các chỉ mục cơ sở dữ liệu thường sử dụng cấu trúc dữ liệu dựa trên nguyên lý tìm kiếm nhị phân như B-tree hoặc B+ tree. Những cấu trúc này cho phép tìm kiếm nhanh chóng trong tập dữ liệu lớn được lưu trữ trên đĩa.
Ví dụ: Khi bạn tìm kiếm một người dùng theo ID trong cơ sở dữ liệu có hàng triệu bản ghi, chỉ mục B-tree cho phép hệ thống nhanh chóng thu hẹp phạm vi tìm kiếm mà không cần quét toàn bộ dữ liệu.
2. Tìm kiếm trong từ điển
Khi bạn tìm một từ trong từ điển điện tử, thuật toán tìm kiếm nhị phân được sử dụng rộng rãi nhờ tính hiệu quả của nó.
Ví dụ: Từ điển có 100,000 từ, tìm kiếm nhị phân chỉ cần khoảng 17 bước so sánh để tìm ra từ bạn cần, trong khi tìm kiếm tuyến tính có thể phải kiểm tra đến 50,000 từ (trung bình).
3. Giải quyết phương trình
Phương pháp chia đôi (bisection method) trong giải tích số sử dụng nguyên lý tìm kiếm nhị phân để tìm nghiệm của phương trình f(x) = 0 trong một khoảng xác định.
Ví dụ: Để tìm nghiệm của phương trình x³ – x – 1 = 0 trong khoảng [1, 2]:
double findRoot(double left, double right, double epsilon) {
while (right - left > epsilon) {
double mid = left + (right - left) / 2;
double f_mid = mid*mid*mid - mid - 1;
if (abs(f_mid) < epsilon) return mid;
if (f_mid * (left*left*left - left - 1) < 0)
right = mid;
else
left = mid;
}
return (left + right) / 2;
}4. Tối ưu hóa
Trong nhiều bài toán tối ưu, tìm kiếm nhị phân được sử dụng để thu hẹp không gian tìm kiếm.
Ví dụ: Tìm giá trị lớn nhất của x sao cho f(x) <= k
int findMaxValue(vector<int>& arr, int k) {
int left = 0, right = arr.size() - 1;
int result = -1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (f(arr[mid]) <= k) {
result = arr[mid];
left = mid + 1; // Tìm giá trị lớn hơn
} else {
right = mid - 1;
}
}
return result;
}5. Thuật toán nén dữ liệu
Một số thuật toán nén sử dụng tìm kiếm nhị phân để tìm kiếm mẫu trong từ điển nén.
Ví dụ: Thuật toán LZW sử dụng bảng mã để nén dữ liệu, và tìm kiếm nhị phân có thể được sử dụng để tìm kiếm các mẫu trong bảng mã này.
Các lỗi thường gặp và cách khắc phục
1. Tràn số khi tính chỉ số giữa
Lỗi: Khi tính mid = (left + right) / 2, có thể xảy ra tràn số nếu left + right vượt quá giới hạn của kiểu dữ liệu.
Khắc phục: Sử dụng công thức mid = left + (right - left) / 2.
2. Vòng lặp vô hạn
Lỗi: Nếu không cập nhật đúng left và right, có thể dẫn đến vòng lặp vô hạn.
Khắc phục: Đảm bảo phạm vi tìm kiếm luôn thu hẹp sau mỗi lần lặp.
3. Điều kiện dừng không chính xác
Lỗi: Sử dụng left < right thay vì left <= right có thể bỏ sót phần tử cuối cùng.
Khắc phục: Sử dụng điều kiện left <= right để đảm bảo xét tất cả các phần tử.
4. Áp dụng cho mảng chưa sắp xếp
Lỗi: Áp dụng tìm kiếm nhị phân cho mảng chưa được sắp xếp.
Khắc phục: Luôn đảm bảo mảng đã được sắp xếp trước khi áp dụng tìm kiếm nhị phân.
// Đảm bảo mảng đã sắp xếp trước khi tìm kiếm
#include <algorithm> // Để sử dụng hàm sort
vector<int> arr = {5, 2, 8, 12, 3};
sort(arr.begin(), arr.end()); // Sắp xếp mảng trước
int result = binarySearch(arr, target);Bài tập thực hành
Để hiểu sâu hơn về thuật toán tìm kiếm nhị phân, hãy thử giải các bài tập sau:
1. Bài tập cơ bản: Viết hàm tìm kiếm nhị phân
Yêu cầu: Viết hàm tìm kiếm nhị phân để tìm một số trong mảng đã sắp xếp.
Lời giải:
int binarySearch(vector<int>& arr, int target) {
int left = 0;
int right = arr.size() - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) return mid;
if (arr[mid] > target) right = mid - 1;
else left = mid + 1;
}
return -1;
}2. Bài tập trung bình: Tìm vị trí đầu tiên và cuối cùng
Yêu cầu: Tìm vị trí đầu tiên và cuối cùng của một số trong mảng đã sắp xếp có phần tử trùng lặp.
Lời giải: Xem phần “Tìm phần tử đầu tiên và cuối cùng” ở trên.
3. Bài tập nâng cao: Tìm phần tử nhỏ nhất trong mảng đã xoay
Yêu cầu: Sử dụng tìm kiếm nhị phân để tìm phần tử nhỏ nhất trong một mảng đã được xoay (rotated sorted array). Ví dụ: [4, 5, 6, 7, 0, 1, 2] là một mảng đã xoay của [0, 1, 2, 4, 5, 6, 7].
Gợi ý:
- Trong mảng đã xoay, phần tử nhỏ nhất là điểm “gãy” của mảng
- Hãy so sánh phần tử giữa với phần tử cuối cùng để xác định nửa nào chứa điểm gãy
- Nếu phần tử giữa lớn hơn phần tử cuối, phần tử nhỏ nhất nằm ở nửa phải
- Nếu phần tử giữa nhỏ hơn phần tử cuối, phần tử nhỏ nhất nằm ở nửa trái hoặc chính là phần tử giữa
Lời giải:
// Tìm phần tử nhỏ nhất trong mảng đã xoay
int findMinInRotatedArray(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
// Nếu mảng không xoay hoặc chỉ có một phần tử
if (right < left) return nums[0];
if (right == left) return nums[left];
// Nếu mảng đã xoay
while (left < right) {
int mid = left + (right - left) / 2;
// Nếu phần tử giữa lớn hơn phần tử bên phải
// thì phần tử nhỏ nhất nằm ở nửa phải
if (nums[mid] > nums[right]) {
left = mid + 1;
}
// Ngược lại, phần tử nhỏ nhất nằm ở nửa trái hoặc chính là mid
else {
right = mid;
}
}
return nums[left];
}Thực hành nhiều bài tập hơn tại luyencode.net
Kết luận
Thuật toán tìm kiếm nhị phân là một công cụ mạnh mẽ trong bộ công cụ của mọi lập trình viên. Với độ phức tạp O(log n), nó mang lại hiệu suất vượt trội so với tìm kiếm tuyến tính khi làm việc với dữ liệu đã sắp xếp.
Những điểm quan trọng cần nhớ:
- Tìm kiếm nhị phân chỉ áp dụng cho dữ liệu đã sắp xếp
- Độ phức tạp thời gian là O(log n), giúp xử lý hiệu quả với dữ liệu lớn
- Có thể triển khai bằng đệ quy hoặc vòng lặp
- Có nhiều biến thể và ứng dụng thực tế
Việc nắm vững thuật toán tìm kiếm nhị phân không chỉ giúp bạn giải quyết các bài toán tìm kiếm cơ bản mà còn là nền tảng để hiểu và áp dụng nhiều thuật toán phức tạp hơn trong tương lai.
Hãy thực hành thường xuyên và áp dụng thuật toán này vào các bài toán thực tế để trở thành một lập trình viên giỏi hơn!






