Kiểm tra số nguyên tố trong C/C++: Từ cơ bản đến tối ưu

Byadmin
0 Comments

Số nguyên tố là một khái niệm cơ bản và quan trọng trong toán học và khoa học máy tính. Một số nguyên tố là số tự nhiên lớn hơn 1 và chỉ có đúng hai ước số là 1 và chính nó.

Ví dụ các số nguyên tố đầu tiên: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97…

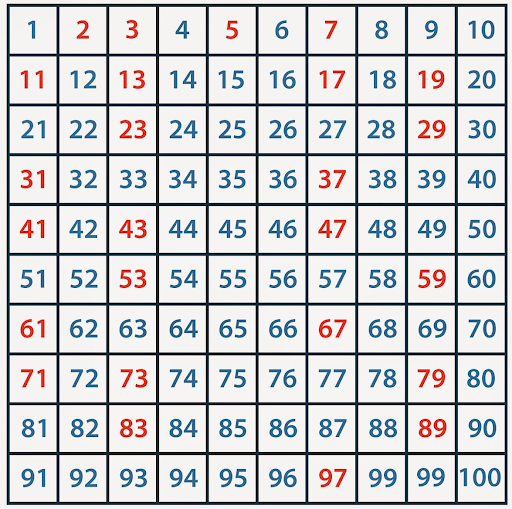
Các số nguyên tố trong phạm vi 1000

Số nguyên tố có nhiều ứng dụng thực tế, đặc biệt trong:

  • Mật mã học: Nền tảng của hệ thống mã hóa RSA và nhiều thuật toán mã hóa khác
  • Lý thuyết số: Cơ sở cho nhiều định lý và nghiên cứu toán học
  • Sinh số ngẫu nhiên: Được dùng trong các thuật toán tạo số giả ngẫu nhiên
  • Bảng băm: Cấu trúc dữ liệu sử dụng số nguyên tố để giảm đụng độ

Trong bài viết này, chúng ta sẽ tìm hiểu các phương pháp kiểm tra số nguyên tố từ đơn giản đến phức tạp, cùng với phân tích hiệu suất và ứng dụng thực tế của từng phương pháp.

🔍 Bạn sẽ học được:

  • Các phương pháp kiểm tra số nguyên tố từ cơ bản đến nâng cao
  • Lý thuyết và nguyên lý hoạt động của mỗi thuật toán
  • Cách triển khai cụ thể trong C/C++
  • Khi nào nên sử dụng phương pháp nào

Cách 1: Kiểm tra số nguyên tố (đơn giản)

Nguyên lý

Phương pháp đơn giản nhất để kiểm tra một số có phải là số nguyên tố hay không dựa trực tiếp vào định nghĩa: một số nguyên tố chỉ chia hết cho 1 và chính nó.

Vì vậy, chúng ta sẽ kiểm tra xem số n có chia hết cho bất kỳ số nào từ 2 đến n-1 hay không. Nếu không chia hết cho số nào trong khoảng này, thì n là số nguyên tố.

Cài đặt

#include <iostream>
using namespace std;

bool isPrime(int n) {
    // Trường hợp đặc biệt
    if (n <= 1) {
        return false;    // 0 và 1 không phải số nguyên tố
    }
    
    // Kiểm tra từ 2 đến n-1
    for (int i = 2; i < n; i++) {
        if (n % i == 0) {
            return false;    // Nếu n chia hết cho i, n không phải số nguyên tố
        }
    }
    
    return true;    // Nếu không chia hết cho số nào, n là số nguyên tố
}

int main() {
    int n;
    cout << "Enter n: ";
    cin >> n;
    
    if (isPrime(n)) {
        cout << n << " is prime number." << endl;
    } else {
        cout << n << " not a prime number." << endl;
    }
    
    return 0;
}

Phân tích

Ưu điểm:

  • ✅ Dễ hiểu, dễ cài đặt
  • ✅ Trực quan, theo sát định nghĩa

Nhược điểm:

  • ❌ Hiệu suất kém với số lớn
  • ❌ Độ phức tạp thời gian: O(n) – không hiệu quả khi n lớn

Ví dụ thực tế:
Với n = 997 (một số nguyên tố), phương pháp này cần kiểm tra 995 số (từ 2 đến 996).

🧠 Suy nghĩ: Đây có phải là cách hiệu quả nhất? Có cần kiểm tra tất cả các số từ 2 đến n-1 không?

Cách 2: Tối ưu vòng lặp đến căn bậc hai

Nguyên lý

Chúng ta có thể cải thiện đáng kể hiệu suất bằng cách chỉ kiểm tra các số từ 2 đến căn bậc hai của n. Để hiểu tại sao, hãy xem xét ví dụ sau:

Giả sử n = 36 và không phải là số nguyên tố. Khi đó n có thể biểu diễn thành tích của hai số: n = a × b

Các cặp ước số của 36:
1 × 36
2 × 18
3 × 12
4 × 9
6 × 6
9 × 4
12 × 3
18 × 2
36 × 1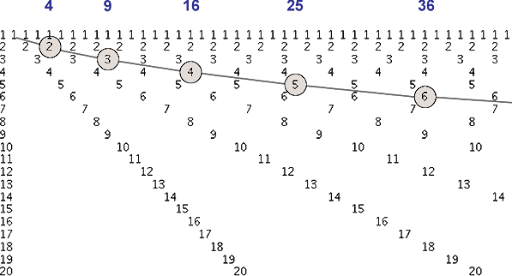
Các cặp ước số luôn gặp nhau tại căn bậc hai

Ta thấy những điều quan trọng:

  1. Các ước số xuất hiện theo cặp (a, b) sao cho a × b = n
  2. Nếu a > √n thì b < √n
  3. Nếu n có ước số, thì ít nhất một ước số phải ≤ √n

Kết luận: Nếu n không có ước số nào trong khoảng từ 2 đến √n, thì n là số nguyên tố!

Cài đặt

#include <iostream>
#include <cmath>
using namespace std;

bool isPrime(int n) {
    // Trường hợp đặc biệt
    if (n <= 1) {
        return false;    // 0 và 1 không phải số nguyên tố
    }
    
    // 2 và 3 là số nguyên tố
    if (n <= 3) {
        return true;
    }
    
    // Kiểm tra nhanh cho số chia hết cho 2 hoặc 3
    if (n % 2 == 0 || n % 3 == 0) {
        return false;
    }
    
    // Kiểm tra từ 5 đến căn bậc hai của n
    // sqrt(n) tính toán căn bậc hai của n
    for (int i = 5; i <= sqrt(n); i += 2) {
        if (n % i == 0) {
            return false;
        }
    }
    
    return true;
}

int main() {
    int n;
    cout << "Enter n: ";
    cin >> n;
    
    if (isPrime(n)) {
        cout << n << " is prime number." << endl;
    } else {
        cout << n << " not a prime number." << endl;
    }
    
    return 0;
}

Phân tích

Ưu điểm:

  • ✅ Hiệu suất tốt hơn nhiều, đặc biệt với số lớn
  • ✅ Độ phức tạp thời gian: O(√n)

Nhược điểm:

  • ❌ Gọi hàm sqrt() trong mỗi lần lặp có thể ảnh hưởng đến hiệu suất
  • ❌ Vẫn kiểm tra nhiều số không cần thiết

Cải tiến:

// Tối ưu hơn: Tính sqrt(n) một lần duy nhất
bool isPrimeOptimized(int n) {
    if (n <= 1) return false;
    if (n <= 3) return true;
    if (n % 2 == 0 || n % 3 == 0) return false;
    
    int sqrtN = sqrt(n);
    for (int i = 5; i <= sqrtN; i += 2) {
        if (n % i == 0) return false;
    }
    
    return true;
}

🧮 So sánh cụ thể:

  • Với n = 997, phương pháp 1 kiểm tra 995 số
  • Với n = 997, phương pháp 2 chỉ kiểm tra khoảng 31 số (√997 ≈ 31.57)

🤔 Thử thách: Bạn có thể chỉ ra tại sao chúng ta bỏ qua các số chẵn (ngoại trừ 2) không cần kiểm tra?

Cách 3: Tối ưu hóa vòng lặp với bước nhảy 6k±1

Nguyên lý

Phương pháp này dựa trên một tính chất toán học:

Tất cả các số nguyên tố lớn hơn 3 đều có dạng 6k ± 1, trong đó k là một số nguyên dương.

Để hiểu tại sao, hãy xem xét các số dưới dạng phân loại theo số dư khi chia cho 6:

  • Số dạng 6k (chia hết cho 6): Không phải số nguyên tố (vì chia hết cho 2 và 3)
  • Số dạng 6k + 2 = 2(3k + 1): Không phải số nguyên tố (vì chia hết cho 2)
  • Số dạng 6k + 3 = 3(2k + 1): Không phải số nguyên tố (vì chia hết cho 3)
  • Số dạng 6k + 4 = 2(3k + 2): Không phải số nguyên tố (vì chia hết cho 2)
  • Số dạng 6k + 1 và 6k + 5 (hay 6k – 1): Có thể là số nguyên tố
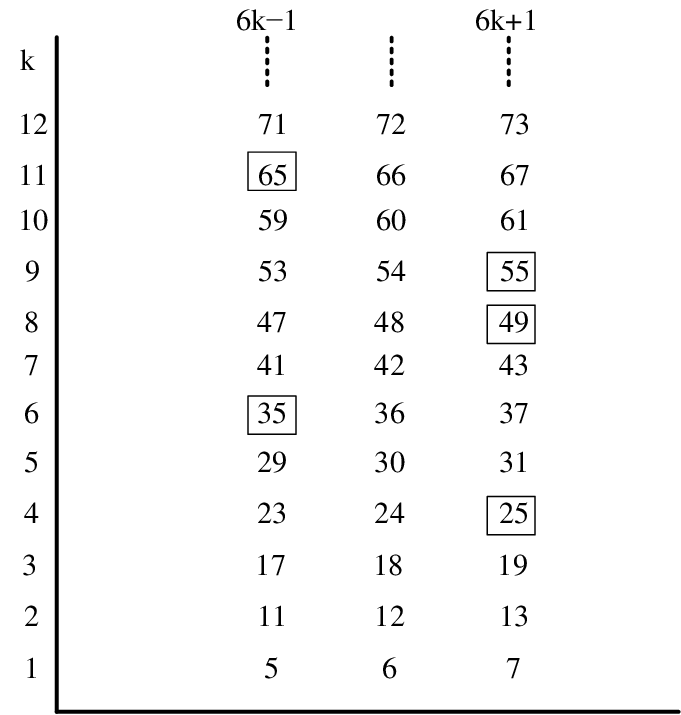
Các số nguyên tố >3 đều có dạng 6k±1

Bảng minh họa:

SốDạngLà số nguyên tố?
56×0+5Có
76×1+1Có
116×1+5Có
136×2+1Có
176×2+5Có
196×3+1Có
236×3+5Có
256×4+1Không (5²)

Lưu ý quan trọng: Không phải tất cả các số có dạng 6k ± 1 đều là số nguyên tố (như số 25 = 6×4+1), nhưng tất cả các số nguyên tố lớn hơn 3 đều có dạng 6k ± 1.

Cài đặt

#include <iostream>
using namespace std;

bool isPrime(int n) {
    // Trường hợp đặc biệt
    if (n <= 1) {
        return false;
    }
    
    // 2 và 3 là số nguyên tố
    if (n <= 3) {
        return true;
    }
    
    // Kiểm tra nhanh cho số chia hết cho 2 hoặc 3
    if (n % 2 == 0 || n % 3 == 0) {
        return false;
    }
    
    // Kiểm tra các số có dạng 6k ± 1
    // i đại diện cho 6k-1 và i+2 đại diện cho 6k+1
    for (int i = 5; i * i <= n; i += 6) {
        if (n % i == 0 || n % (i + 2) == 0) {
            return false;
        }
    }
    
    return true;
}

int main() {
    int n;
    cout << "Enter n: ";
    cin >> n;
    
    if (isPrime(n)) {
        cout << n << " is prime number." << endl;
    } else {
        cout << n << " not a prime number." << endl;
    }
    
    return 0;
}

Phân tích

Ưu điểm:

  • ✅ Hiệu suất tốt hơn phương pháp 2
  • ✅ Giảm số lần lặp (khoảng 1/3 so với phương pháp 2)
  • ✅ Sử dụng i * i <= n thay vì sqrt(n) giúp tránh gọi hàm nhiều lần
  • ✅ Độ phức tạp thời gian: O(√n) nhưng với hằng số nhỏ hơn

Nhược điểm:

  • ❌ Phức tạp hơn về mặt khái niệm
  • ❌ Vẫn chưa thực sự hiệu quả với số rất lớn (>10^9)

🧮 So sánh cụ thể:

  • Với n = 997, phương pháp 2 kiểm tra khoảng 31 số
  • Với n = 997, phương pháp 3 chỉ kiểm tra khoảng 10-11 số (kiểm tra cặp số 5,7 rồi 11,13 rồi 17,19, v.v.)

💡 Hiểu rõ hơn về i và i+2:

  • Khi i = 5: Kiểm tra 5 (6×0+5) và 7 (6×1+1)
  • Khi i = 11: Kiểm tra 11 (6×1+5) và 13 (6×2+1)
  • Khi i = 17: Kiểm tra 17 (6×2+5) và 19 (6×3+1)
  • …

🤔 Thử thách: Tại sao chúng ta không cần kiểm tra n % (i – 2) hoặc các giá trị khác?

Cách 4: Kiểm tra Miller-Rabin

Đây là một thuật toán nâng cao và không nằm trong phạm vi của bài viết này. Bạn đọc quan tâm, vui lòng tìm hiểu tại Miller–Rabin primality test.

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;

// Hàm tính (a^d) % n an toàn với số lớn
long long modPow(long long a, long long d, long long n) {
    long long res = 1;
    a = a % n;
    while (d > 0) {
        // Nếu d lẻ, nhân kết quả với a
        if (d & 1) {
            res = (res * a) % n;
        }
        
        // d = d/2
        d = d >> 1;
        
        // a = a^2
        a = (a * a) % n;
    }
    return res;
}

// Hàm kiểm tra Miller-Rabin một lần
bool millerTest(long long d, long long n) {
    // Chọn một số ngẫu nhiên trong khoảng [2, n-2]
    long long a = 2 + rand() % (n - 4);
    
    // Tính a^d % n
    long long x = modPow(a, d, n);
    
    if (x == 1 || x == n - 1) {
        return true;  // Có thể là số nguyên tố
    }
    
    // Tiếp tục bình phương x khi d chưa bằng n-1
    // và (x^2) % n chưa bằng n-1
    while (d != n - 1) {
        x = (x * x) % n;
        d *= 2;
        
        if (x == 1) {
            return false;  // Chắc chắn là hợp số
        }
        if (x == n - 1) {
            return true;   // Có thể là số nguyên tố
        }
    }
    
    // Chắc chắn là hợp số
    return false;
}

// Hàm kiểm tra số nguyên tố sử dụng Miller-Rabin
bool isPrime(long long n, int k = 5) {
    // Các trường hợp đặc biệt
    if (n <= 1 || n == 4) {
        return false;
    }
    if (n <= 3) {
        return true;
    }
    
    // Tìm d sao cho n-1 = 2^r * d
    // với d là số lẻ
    long long d = n - 1;
    while (d % 2 == 0) {
        d /= 2;
    }
    
    // Thực hiện kiểm tra Miller-Rabin k lần
    for (int i = 0; i < k; i++) {
        if (!millerTest(d, n)) {
            return false;  // Chắc chắn là hợp số
        }
    }
    
    return true;  // Có xác suất cao là số nguyên tố
}

int main() {
    // Khởi tạo seed cho hàm rand()
    srand(time(NULL));
    
    long long n;
    cout << "Enter n: ";
    cin >> n;
    
    if (isPrime(n)) {
        cout << n << " has a high probability of being prime." << endl;
    } else {
        cout << n << " not a prime number." << endl;
    }
    
    return 0;
}

Phân tích

Ưu điểm:

  • ✅ Cực kỳ hiệu quả cho số lớn
  • ✅ Độ phức tạp thời gian: O(k log^3 n), trong đó k là số lần kiểm tra
  • ✅ Đủ chính xác cho hầu hết các ứng dụng thực tế

Nhược điểm:

  • ❌ Phức tạp về mặt khái niệm và cài đặt
  • ❌ Là thuật toán xác suất, có thể cho kết quả sai với xác suất nhỏ
  • ❌ Cần nhiều mã lệnh hơn các phương pháp trước

🔍 Về độ chính xác:

  • Với k = 5 lần kiểm tra, xác suất kết quả sai < 1/4^5 ≈ 0.001%
  • Với k = 10 lần kiểm tra, xác suất kết quả sai < 1/4^10 ≈ 0.000001%
  • Với các số < 2^64, nếu chọn đúng các giá trị a (như 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37), thuật toán cho kết quả chính xác 100%

💡 Ứng dụng thực tế:

  • Kiểm tra số nguyên tố trong mật mã RSA
  • Sinh số nguyên tố lớn (ví dụ: 512-bit, 1024-bit, 2048-bit)
  • Các thuật toán mật mã khác yêu cầu số nguyên tố lớn

Cách 5: Sàng Eratosthenes

Nguyên lý

Sàng Eratosthenes là một thuật toán cổ điển để tìm tất cả các số nguyên tố nhỏ hơn hoặc bằng một số n cho trước. Phương pháp này đặc biệt hiệu quả khi cần tìm nhiều số nguyên tố trong một khoảng.

Bài viết chi tiết: Thuật toán sàng nguyên tố Eratosthenes

Kết luận

Trong bài viết này, chúng ta đã tìm hiểu về các phương pháp kiểm tra số nguyên tố từ cơ bản đến nâng cao:

  1. Phương pháp cơ bản: Kiểm tra từ 2 đến n-1, đơn giản nhưng hiệu suất kém.
  2. Phương pháp tối ưu vòng lặp đến căn bậc hai: Cải thiện hiệu suất bằng cách chỉ kiểm tra đến căn bậc hai của n.
  3. Phương pháp tối ưu hóa vòng lặp với bước nhảy: Cải thiện thêm bằng cách chỉ kiểm tra các số có dạng 6k ± 1.
  4. Phương pháp Miller-Rabin: Thuật toán xác suất hiệu quả cho số lớn.
  5. Sàng Eratosthenes: Hiệu quả khi cần kiểm tra nhiều số trong một khoảng.

Mỗi phương pháp có ưu và nhược điểm riêng, và việc lựa chọn phương pháp phù hợp phụ thuộc vào yêu cầu cụ thể của bài toán:

  • Nếu bạn cần kiểm tra một số duy nhất và không quá lớn, phương pháp 2 hoặc 3 là lựa chọn tốt.
  • Nếu bạn cần kiểm tra một số rất lớn, phương pháp Miller-Rabin là lựa chọn tốt nhất.
  • Nếu bạn cần kiểm tra nhiều số trong một khoảng, sàng Eratosthenes là lựa chọn hiệu quả nhất.

Việc hiểu và áp dụng đúng các thuật toán kiểm tra số nguyên tố không chỉ giúp bạn giải quyết các bài toán liên quan đến số nguyên tố một cách hiệu quả, mà còn giúp bạn nâng cao kỹ năng tối ưu hóa thuật toán nói chung.

Câu hỏi thường gặp

1. Tại sao số 1 không phải là số nguyên tố?

Theo định nghĩa, số nguyên tố là số tự nhiên lớn hơn 1 và chỉ có đúng hai ước số là 1 và chính nó. Số 1 chỉ có một ước số là chính nó, nên không thỏa mãn định nghĩa.

2. Làm thế nào để kiểm tra số nguyên tố lớn hơn 10^9?

Đối với số rất lớn, phương pháp Miller-Rabin là lựa chọn tốt nhất. Nó có độ phức tạp thấp và độ chính xác cao.

3. Có thể sử dụng sàng Eratosthenes để kiểm tra số nguyên tố lớn không?

Sàng Eratosthenes không phù hợp để kiểm tra số nguyên tố lớn vì nó tốn nhiều bộ nhớ. Nó chỉ phù hợp để tìm tất cả các số nguyên tố trong một khoảng nhỏ.

4. Làm thế nào để tối ưu hóa thuật toán kiểm tra số nguyên tố cho số lớn?

Ngoài việc sử dụng thuật toán Miller-Rabin, bạn có thể tối ưu hóa thêm bằng cách:

  • Kiểm tra trước các số nguyên tố nhỏ (2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, …)
  • Sử dụng các phép toán bit để tăng tốc độ tính toán
  • Sử dụng các thuật toán song song nếu có thể

5. Có thuật toán nào kiểm tra số nguyên tố nhanh hơn Miller-Rabin không?

Có một số thuật toán khác như AKS (Agrawal-Kayal-Saxena) là thuật toán đa thức và đảm bảo chính xác 100%, nhưng nó phức tạp hơn và thường chậm hơn Miller-Rabin trong thực tế. Đối với hầu hết các ứng dụng, Miller-Rabin với đủ số lần kiểm tra là đủ tốt.

Similar Posts

1000 bài tập lập trình có lời giải

Chinh phục 1000 bài tập lập trình (có lời giải)

Byadmin

Bạn đang tìm kiếm bài tập lập trình? Hôm nay, Luyện Code vô cùng hân hạnh giới thiệu tới các bạn một bộ sưu tập quý giá gồm 1000 bài tập lập trình được biên soạn bởi thầy Nguyễn Tấn Trần Minh Khang – một chuyên gia giàu kinh nghiệm trong lĩnh vực lập trình….

Lấy thời gian hiện tại trong C++ như nào?

Lấy thời gian hiện tại trong C++ như nào?

Byadmin

Truy xuất thời gian hiện tại là một nhu cầu quan trọng trong hầu hết các ứng dụng phần mềm hiện đại. Từ việc ghi nhật ký sự kiện, tính toán thời gian thực thi, đến việc lên lịch các tác vụ, xử lý thời gian đều đóng vai trò thiết yếu. Trong C++, chúng…

Thuật toán tìm kiếm nhị phân

Tìm kiếm nhị phân – Giải thuật kinh điển cần biết

Byadmin

Thuật toán tìm kiếm nhị phân là một trong những thuật toán tìm kiếm hiệu quả nhất trong khoa học máy tính. Với độ phức tạp O(log n), thuật toán này đặc biệt phù hợp với các tập dữ liệu lớn đã được sắp xếp. Bằng cách liên tục chia đôi phạm vi tìm kiếm…

Tìm số lớn thứ 2 trong mảng 1 chiều

Tìm số lớn thứ 2 trong mảng 1 chiều

Byadmin

Tìm số lớn thứ 2 trong mảng là một bài toán phổ biến trong lập trình, thường xuất hiện trong các cuộc phỏng vấn và các kỳ thi lập trình. Bài viết này sẽ hướng dẫn bạn cách giải quyết bài toán này một cách hiệu quả nhất. Giới thiệu bài toán Bài toán tìm…

0 0 votes
Article Rating
Subscribe
Notify of
guest
0 Comments
Oldest
Newest Most Voted
Inline Feedbacks
View all comments