Thuật toán sàng nguyên tố Eratosthenes
Thuật toán sàng nguyên tố Eratosthenes là phương pháp hiệu quả để tìm tất cả các số nguyên tố nhỏ hơn hoặc bằng một số N.
- Có độ phức tạp thời gian O(n log log n) và độ phức tạp không gian O(n)
- Nguyên lý: Đánh dấu các bội số của mỗi số nguyên tố để loại bỏ các số hợp số.
- Phương pháp này vượt trội so với kiểm tra từng số (độ phức tạp O(n√n)).
- Có nhiều cải tiến như sàng phân đoạn và sàng tuyến tính để tối ưu hiệu suất.
Giới thiệu
Số nguyên tố là một khái niệm cơ bản và quan trọng trong toán học. Chúng là những số tự nhiên lớn hơn 1 chỉ có đúng hai ước số là 1 và chính nó. Việc tìm số nguyên tố có nhiều ứng dụng quan trọng, đặc biệt trong mật mã học và bảo mật thông tin.
Tuy nhiên, việc kiểm tra một số có phải là số nguyên tố hay không, hoặc tìm tất cả các số nguyên tố trong một khoảng cho trước có thể trở nên rất tốn kém về mặt tính toán khi số lượng phần tử tăng lên. Đây chính là lúc thuật toán sàng Eratosthenes phát huy tác dụng!
Nguyên lý hoạt động
Thuật toán sàng Eratosthenes là một phương pháp hiệu quả để tìm tất cả các số nguyên tố nhỏ hơn hoặc bằng một số N cho trước. Ý tưởng chính của thuật toán rất đơn giản và thông minh:
- Tạo một danh sách các số từ 2 đến n.
- Bắt đầu từ số 2 (số nguyên tố nhỏ nhất).
- Đánh dấu tất cả các bội của số hiện tại (trừ chính nó).
- Tìm số chưa bị đánh dấu tiếp theo và lặp lại bước 3.
- Quá trình kết thúc khi đã xét đến căn bậc hai của N.
Sau khi thuật toán kết thúc, các số chưa bị đánh dấu chính là các số nguyên tố. Bạn có thể xem ảnh GIF dưới đây để hiểu rõ hơn cơ chế hoạt động của thuật toán.
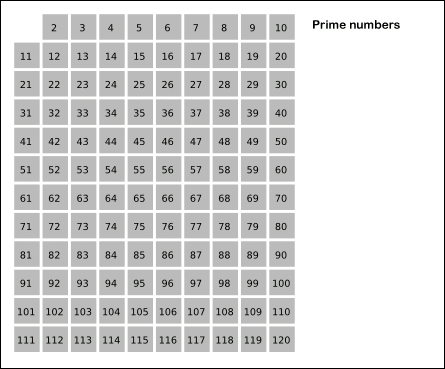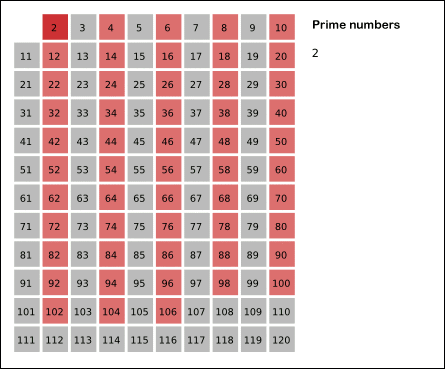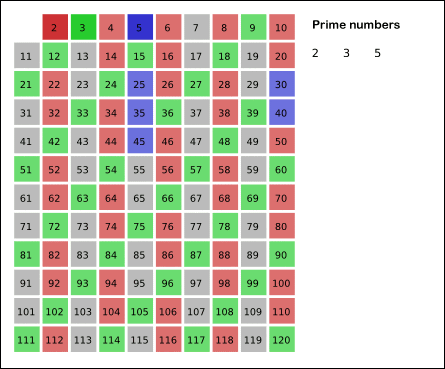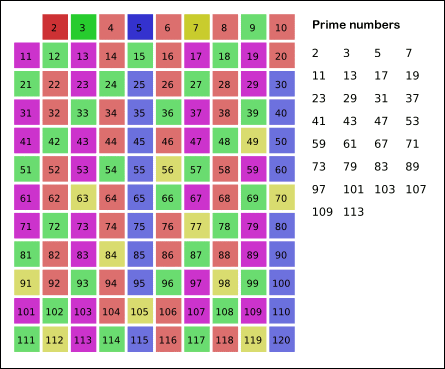
Cài đặt thuật toán
Phiên bản cơ bản (C++)
Sàng nguyên tố phiên bản cơ bản sử dụng một mảng boolean để đánh dấu các số nguyên tố. Ưu điểm của cách này là dễ hiểu và dễ cài đặt:
- Sử dụng vector<bool> để tối ưu bộ nhớ (C++ tự động nén dữ liệu boolean).
- Chỉ duyệt đến căn bậc hai của n để tăng hiệu suất.
- Bắt đầu đánh dấu từ
i*ithay vì2*iđể tránh đánh dấu trùng lặp.
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
vector<bool> sieveOfEratosthenes(int n) {
// Khởi tạo mảng đánh dấu
vector<bool> isPrime(n + 1, true);
isPrime[0] = isPrime[1] = false; // 0 và 1 không phải số nguyên tố
// Thực hiện sàng
for (int i = 2; i <= sqrt(n); i++) {
if (isPrime[i]) {
// Đánh dấu các bội của i
for (int j = i * i; j <= n; j += i) {
isPrime[j] = false;
}
}
}
return isPrime;
}
// Hàm in các số nguyên tố
void printPrimes(const vector<bool>& isPrime) {
cout << "Prime numbers are: ";
for (int i = 2; i < isPrime.size(); i++) {
if (isPrime[i]) {
cout << i << " ";
}
}
cout << endl;
}
int main() {
int n;
cout << "Enter n: ";
cin >> n;
vector<bool> primes = sieveOfEratosthenes(n);
printPrimes(primes);
return 0;
}Phiên bản tối ưu (Chỉ sàng số lẻ)
Phiên bản tối ưu cải thiện hiệu suất so với sàng nguyên tố cơ bản bằng cách:
- Chỉ xét và đánh dấu các số lẻ, giảm một nửa không gian bộ nhớ và số phép tính.
- Sử dụng vector<int> để lưu trực tiếp các số nguyên tố thay vì đánh dấu.
- Xử lý số 2 riêng vì là số nguyên tố chẵn duy nhất.
- Sử dụng kiểu long long cho các phép nhân để tránh tràn số với N lớn.
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
vector<int> optimizedSieve(int n) {
// Khởi tạo kết quả và đưa số 2 vào (số nguyên tố chẵn duy nhất)
vector<int> primes;
if (n >= 2) primes.push_back(2);
// Chỉ xét các số lẻ
vector<bool> isPrime((n-1)/2 + 1, true);
// Thực hiện sàng
for (int i = 3; i <= n; i += 2) {
// Lấy chỉ số trong mảng isPrime
int idx = (i-3)/2;
if (isPrime[idx]) {
primes.push_back(i);
// Chỉ đánh dấu các số lẻ
for (long long j = (long long)i * i; j <= n; j += 2 * i) {
int mark_idx = (j-3)/2;
if (mark_idx < isPrime.size()) {
isPrime[mark_idx] = false;
}
}
}
}
return primes;
}
int main() {
int n;
cout << "Enter n: ";
cin >> n;
vector<int> primes = optimizedSieve(n);
cout << "Prime numbers <= " << n << " are: ";
for (int p : primes) {
cout << p << " ";
}
cout << endl;
cout << "Total: " << primes.size() << " prime numbers" << endl;
return 0;
}def sieve_of_eratosthenes(n):
# Khởi tạo mảng đánh dấu
is_prime = [True for i in range(n+1)]
is_prime[0] = is_prime[1] = False
# Thực hiện sàng
p = 2
while p * p <= n:
# Nếu p là số nguyên tố, đánh dấu các bội của p
if is_prime[p]:
for i in range(p * p, n+1, p):
is_prime[i] = False
p += 1
# Trả về danh sách các số nguyên tố
return [p for p in range(2, n+1) if is_prime[p]]
# Sử dụng
n = int(input("Enter n: "))
primes = sieve_of_eratosthenes(n)
print(f"Prime numbers <= {n} are:", primes)
print(f"Total: {len(primes)} prime numbers")Đánh giá độ phức tạp thuật toán sàng nguyên tố:
- Độ phức tạp thời gian của thuật toán sàng Eratosthenes là O(n log log n).
- Độ phức tạp không gian là O(n), do cần một mảng boolean kích thước n để đánh dấu các số.
So sánh các phương pháp tìm số nguyên tố
| Phương pháp | Độ phức tạp thời gian | Độ phức tạp không gian | Ưu điểm | Nhược điểm |
|---|---|---|---|---|
| Kiểm tra từng số | O(n√n) | O(1) | Đơn giản, ít bộ nhớ | Chậm với n lớn |
| Sàng Eratosthenes | O(n log log n) | O(n) | Nhanh cho đến n = 10⁸ | Tốn bộ nhớ với n lớn |
| Sàng phân đoạn | O(n log log n) | O(√n) | Tiết kiệm bộ nhớ | Phức tạp về mặt cài đặt |
| Sàng tuyến tính | O(n) | O(n) | Nhanh nhất về lý thuyết | Khó cài đặt |
Dưới đây là kết quả so sánh tham khảo cho thời gian chạy của các phương pháp khác nhau (đo bằng mili giây):
| n | Kiểm tra từng số | Sàng Eratosthenes | Sàng phân đoạn | Sàng tuyến tính |
|---|---|---|---|---|
| 10⁴ | 45 ms | 1 ms | 2 ms | 1 ms |
| 10⁵ | 1,420 ms | 6 ms | 7 ms | 4 ms |
| 10⁶ | 45,230 ms | 45 ms | 52 ms | 38 ms |
| 10⁷ | > 1 giờ | 420 ms | 450 ms | 380 ms |
| 10⁸ | > 10 giờ | 4,500 ms | 4,200 ms | 3,800 ms |
Ứng dụng thực tế
1. Mật mã học
Số nguyên tố là nền tảng cho nhiều hệ thống mã hóa, đặc biệt là RSA. Dưới đây là ví dụ đơn giản về cách tạo khóa RSA:
import random
from math import gcd
# Sử dụng sàng để tạo danh sách số nguyên tố
primes = sieve_of_eratosthenes(1000) # Tìm số nguyên tố đến 1000
# Chọn hai số nguyên tố ngẫu nhiên
p = random.choice(primes)
q = random.choice(primes)
while p == q: # Đảm bảo p và q khác nhau
q = random.choice(primes)
# Tính n = p*q
n = p * q
# Tính phi(n) = (p-1)*(q-1)
phi = (p - 1) * (q - 1)
# Chọn e sao cho 1 < e < phi(n) và gcd(e, phi(n)) = 1
e = 65537 # Giá trị e phổ biến trong RSA
while gcd(e, phi) != 1:
e = random.choice(range(3, phi, 2))
# Tìm d sao cho (d*e) % phi = 1
def mod_inverse(e, phi):
for d in range(3, phi):
if (d * e) % phi == 1:
return d
return None
d = mod_inverse(e, phi)
print(f"Khóa công khai: (n={n}, e={e})")
print(f"Khóa bí mật: (n={n}, d={d})")2. Lý thuyết số
Thuật toán sàng giúp nghiên cứu phân bố số nguyên tố và kiểm chứng các giả thuyết trong lý thuyết số.
3. Thi đấu lập trình
Rất nhiều bài toán trong các kỳ thi lập trình liên quan đến số nguyên tố và yêu cầu thuật toán hiệu quả.
Ví dụ:
Cải tiến thuật toán
1. Sàng phân đoạn (Segmented Sieve)
Sàng phân đoạn giải quyết vấn đề bộ nhớ khi n rất lớn bằng cách chia khoảng [2, n] thành các đoạn nhỏ hơn và áp dụng thuật toán sàng nguyên tố cho từng đoạn.
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
vector<int> segmentedSieve(int n) {
int limit = sqrt(n) + 1;
// Tìm tất cả số nguyên tố đến căn bậc hai của n
vector<int> primes = optimizedSieve(limit);
vector<int> result(primes);
// Xử lý từng đoạn
int low = limit;
int high = 2 * limit;
while (low < n) {
if (high > n) high = n;
// Khởi tạo mảng đánh dấu cho đoạn [low, high]
vector<bool> mark(high - low + 1, true);
// Đánh dấu các bội của số nguyên tố đã biết
for (int prime : primes) {
// Tìm bội đầu tiên của prime trong đoạn [low, high]
int loLim = (low / prime) * prime;
if (loLim < low) loLim += prime;
if (loLim == prime) loLim += prime; // Bỏ qua chính số nguyên tố
// Đánh dấu các bội của prime trong đoạn
for (int j = loLim; j <= high; j += prime)
mark[j - low] = false;
}
// Các số chưa bị đánh dấu là số nguyên tố
for (int i = low; i <= high; i++)
if (mark[i - low]) result.push_back(i);
// Chuyển sang đoạn tiếp theo
low = high + 1;
high = low + limit - 1;
}
return result;
}Sàng tuyến tính (Linear Sieve)
Sàng tuyến tính có độ phức tạp O(n) và đảm bảo mỗi số hợp số chỉ bị đánh dấu một lần.
#include <iostream>
#include <vector>
using namespace std;
vector<int> linearSieve(int n) {
vector<int> lp(n + 1, 0); // Số nguyên tố nhỏ nhất chia hết
vector<int> primes;
for (int i = 2; i <= n; ++i) {
if (lp[i] == 0) {
lp[i] = i;
primes.push_back(i);
}
for (int j = 0; j < (int)primes.size() && primes[j] <= lp[i] && i * primes[j] <= n; ++j)
lp[i * primes[j]] = primes[j];
}
return primes;
}Các câu hỏi thường gặp (FAQ)
1. Tại sao chỉ cần sàng đến căn bậc hai của n?
Trả lời: Nếu một số x > √n là hợp số, thì nó phải có ít nhất một ước số p ≤ √n. Số p này sẽ đánh dấu x trong quá trình sàng, nên ta không cần xét các số lớn hơn √n.
2. Thuật toán sàng nguyên tố gặp vấn đề gì với số rất lớn?
Trả lời: Với n rất lớn (> 10⁹), thuật toán cơ bản sẽ tốn quá nhiều bộ nhớ. Giải pháp là sử dụng sàng phân đoạn hoặc các thuật toán xác suất như Miller-Rabin.
3. Làm sao tìm số nguyên tố thứ n?
Trả lời: Sử dụng sàng nguyên tố để tạo danh sách số nguyên tố, sau đó truy cập phần tử thứ n (đánh số từ 0). Theo định lý số nguyên tố, số nguyên tố thứ n xấp xỉ n×ln(n).
4. Thuật toán có phù hợp để kiểm tra tính nguyên tố của một số duy nhất không?
Trả lời: Không. Với một số duy nhất, thuật toán kiểm tra nguyên tố như Miller-Rabin hoặc kiểm tra căn bậc hai sẽ hiệu quả hơn.
5. Các lỗi thường gặp khi cài đặt?
Trả lời:
- Tràn số khi n lớn (cần sử dụng kiểu long long)
- Giới hạn bộ nhớ (cần sử dụng sàng phân đoạn)
- Bắt đầu đánh dấu từ p thay vì p² (không tối ưu)
- Quên đánh dấu 0 và 1 không phải số nguyên tố
Kết luận
Thuật toán sàng nguyên tố Eratosthenes là một công cụ mạnh mẽ trong việc tìm số nguyên tố. Với độ phức tạp thời gian O(n log log n), nó là một trong những thuật toán hiệu quả nhất cho bài toán này. Mặc dù có một số hạn chế về mặt bộ nhớ, nhưng với các cải tiến hiện đại như sàng phân đoạn và sàng tuyến tính, thuật toán vẫn được sử dụng rộng rãi trong nhiều ứng dụng thực tế.
Hiểu và vận dụng tốt thuật toán sàng Eratosthenes không chỉ giúp bạn giải quyết hiệu quả các bài toán liên quan đến số nguyên tố, mà còn là nền tảng để tiếp cận các thuật toán phức tạp hơn trong lý thuyết số.
Tài liệu tham khảo
- Introduction to Algorithms (CLRS) – Chapter 33: Number-Theoretic Algorithms
- Competitive Programming 3 – Steven Halim – Chapter 5: Mathematics
- Number Theory for Competitive Programming
- Mathematics for Computer Science – MIT OpenCourseWare
- Prime Numbers and Computer Methods for Factorization – Hans Riesel
- Elementary Number Theory – David M. Burton






