Ở bài trước, chúng ta đã hoàn thành việc insert một Node vào Red Back Tree. Còn bây giờ, hãy cũng tìm cách để xóa một node khỏi cây đỏ đen nào.
Xóa (Delete) là một quá trình cực kì phức tạp. Mình đã phải tham khảo rất nhiều nguồn mới hoàn thành bài code hoàn chỉnh. Do đó, các bạn nên đọc kĩ tất cả và không nên bỏ qua bất cứ phần nào.
NỘI DUNG BÀI VIẾT
1. Nâng cấp hàm quay cây – Update Rotate
Tại sao phải nâng cấp?
Như các bạn đã biết, Red Black Tree có một phần tử đặc biệt – đó là Root (luôn luôn mang màu đen). Do đó khi lỡ xóa Root thì ta phải đặt lại Root mới. Mà muốn có được Root thì ta phải đưa hai hàm rotateRight và rotateLeft vào struct Red Black Tree:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
struct RedBlackTree { Node* Root; Node* rotateRight(Node* root) { Node* x = root->left; // Gán x->right vào left root root->left = x->right; if (x->right != NULL) x->right->parent = root; x->parent = root->parent; if (root->parent == NULL) Root = x; else if (root->parent->left == root) root->parent->left = x; else root->parent->right = x; // Gán root vào x.right x->right = root; root->parent = x; // Trả về x return x; } Node* rotateLeft(Node* root) { Node* y = root->right; // Gán y->left vào right root root->right = y->left; if (y->left != NULL) y->left->parent = root; y->parent = root->parent; if (root->parent == NULL) Root = y; else if (root->parent->left == root) root->parent->left = y; else root->parent->right = y; // Gán root vào y.left y->left = root; root->parent = y; // Trả về y; return y; } |
2. Sơ lược về cách xóa ở cây đỏ đen
- Khi xóa một Node ở Binary Search Tree, chúng ta chưa bao giờ thực sự một Node có hai con cả. Mà tìm một Node khác để xóa (lớn nhất bên trái) rồi quy về trường hợp (có một con) hoặc (có 0 con – lá). Như vậy, quy ước:
- vDelete: Là node bị xóa (Đôi khi gọi tắt là Node v)
- uReplace: Là sẽ thay thế vDelete (u có thể bằng NULL vì nó cũng là một Node đen)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
void deleteNode(Node* vDelete) { Node* uReplace; if ((vDelete->left != NULL) && (vDelete->right != NULL)) uReplace = maxValueNode(vDelete->left); else if (vDelete->left != NULL) uReplace = vDelete->left; else if (vDelete->right != NULL) uReplace = vDelete->right; else uReplace = NULL; bool uvBlack = ((uReplace == NULL) || (uReplace->color == 0)) && (vDelete->color == 0); Node* par = vDelete->parent; Node* sib = sibling(vDelete); if (uReplace == NULL) { // Do Something } if (vDelete->left == NULL || vDelete->right == NULL) { // Do Someting } // Nếu qua hai trường hợp trên mà vẫn không làm gì cả. // Có nghĩa là vDelete có cả 2 con khác NULL. // Ta tiến hành swap giá trị uReplace và vDelete cho nhau // Rồi xóa uReplace mang giá trị của vDelete swapValues(uReplace, vDelete); deleteNode(uReplace); } |
-
- Khi chúng ta lỡ xóa đi một Node đen: sẽ có ít nhất một đường dẫn bị giảm số lượng Node đen đi 1. Điều đó làm vi phạm quy tắc số 4 – Mọi đường dẫn từ một node đến bất kì node NULL (thuộc con của nó ) thì đều có cùng số lượng node đen.
-
- Nếu vDelete hoặc uReplace màu đỏ: Ta chỉ đơn giản xóa đi Node màu đỏ với giá trị data của vDelete. Việc này hoàn toàn không vi phạm quy tắc trên. Do đó, đây được coi là trường hợp dễ nhất. (u và v không thể cùng màu đỏ vì theo quy tắc 3 – không có hai node đỏ liền kề)
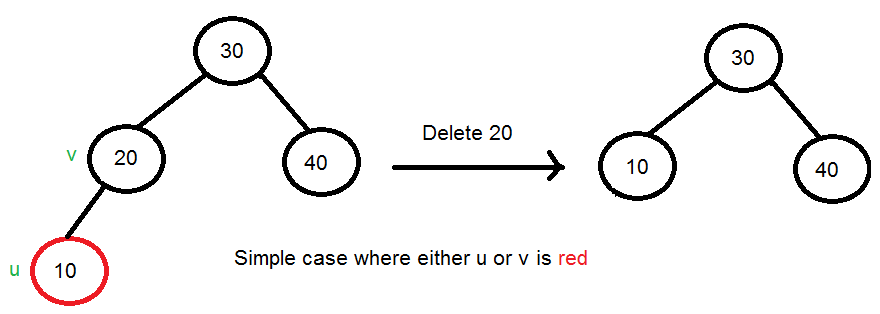
-
- Nếu vDelete và uReplace màu đen: Khi một nút màu đen bị xóa (v) và được thay thế bằng nút con màu đen (u), nút con đó (u) được đánh dấu là nút đen đôi . Nhiệm vụ chính bây giờ trở thành chuyển đổi màu đen đôi này thành màu đen đơn.
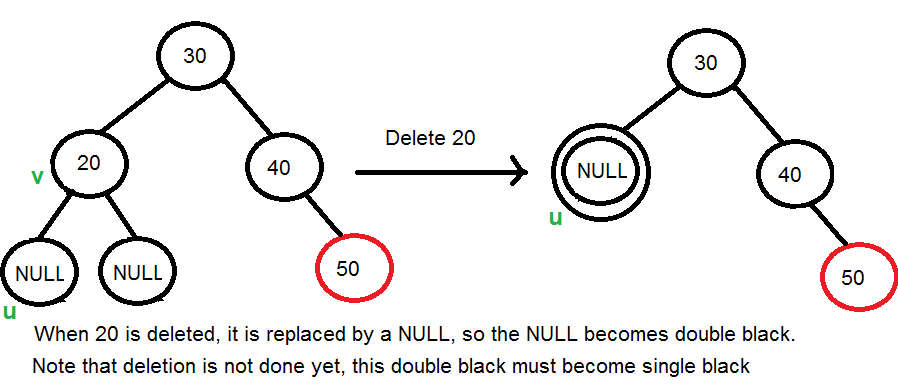
3. Xử lí trường hợp đen đôi – fixDoubleBlack
Note: Đên đôi + Đỏ đơn = Đen Đơn Ở bài trước, chúng ta phân chia các trường hợp dựa vào vị trí của Node X được thêm vào và cha của nó. Còn bây giờ, không hề có Node mới nào. Do đó ta phải dựa chia các trường hợp dựa trên Node Anh Em (sibling) của Node bị xóa (vDelete). Cách tìm Node Anh Em (sibling) cũng khá đơn giản vì nó có cùng cha với vDelete:
|
1 2 3 4 5 6 7 |
Node* sibling(Node* current) { if (current->parent == NULL) return NULL; if (current->parent->left == current) return current->parent->right; return current->parent->left; } |
Mình sẽ viết thêm một hàm hỗ trợ với mục đích là kiểm tra một Node có con màu đỏ hay không – hasRedChild()
|
1 2 3 4 5 6 7 8 9 |
bool hasRedChild(Node* x) { if (x->right != NULL) if (x->right->color == 1) return true; if (x->left != NULL) if (x->left->color == 1) return true; return false; } |
Giờ ta chia hàm fixDoubleBlack() ra 4 trường hợp dựa trên Node Anh Em (Sibling):
- Node Anh Em màu đen và có con đỏ.
- Node Anh Em màu đen và không có con đỏ.
- Node Anh Em có màu đỏ.
- Node Anh Em == NULL
|
1 2 3 4 5 6 7 |
void fixDoubleBlack(Node* root) { if (root == Root) return; Node* sib = sibling(root); Node* par = root->parent; //... } |
1. sibing.color == BLACK and hasRedChild(sibling)
Ta cứ dựa trên vị trí Node sib và con đỏ của nó để phân chia các trường hợp con. Khá quen thuộc đó là Left left, Left right, Right right, Right left.
a) Right right case – Phải phải
-
- Xảy ra: sib là con phải__ sib.right->color == RED
- Xử lí:
-
-
- sib.right->color = sib.color.
- sib->color = sib.parent->color
- par->color = BLACK
- rotateLeft(par)
-
-
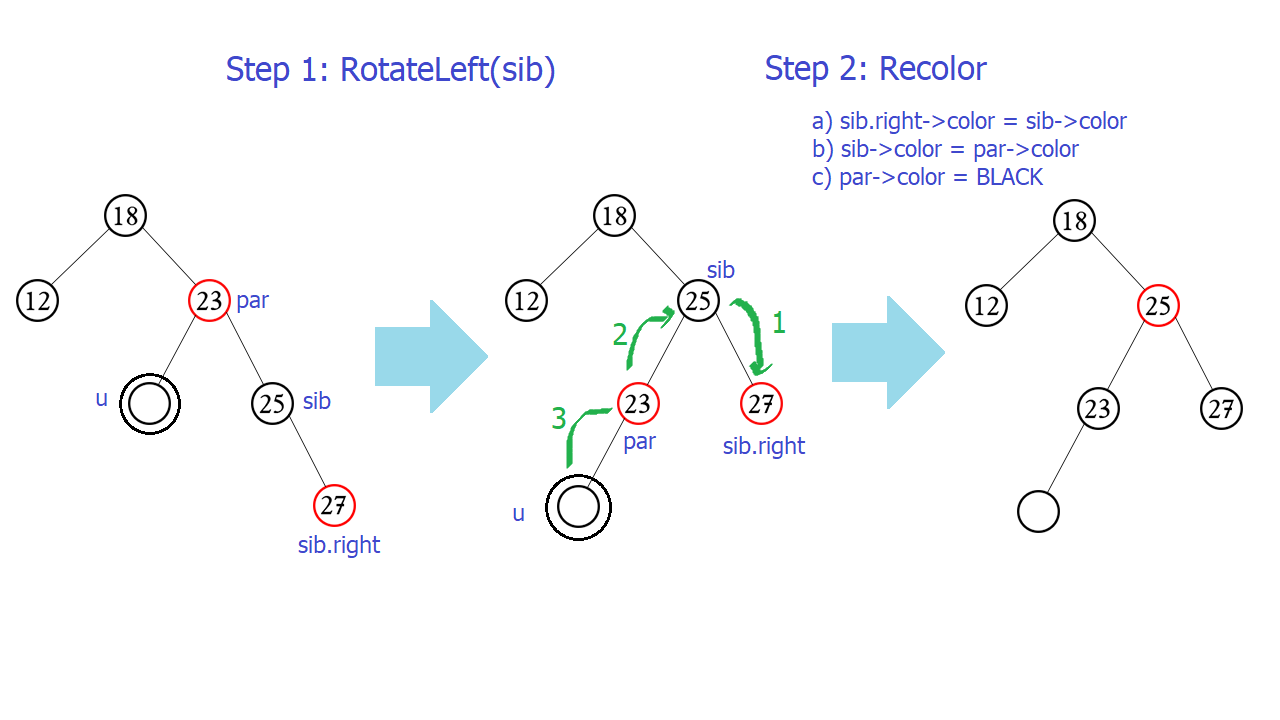
- Khi sib nằm phía bên phải và có con phải màu đỏ (cả 2 con màu đỏ cũng không sao). Ta sẽ coi đây là trường hợp Phải phải và tiến hành quay Trái Node sibling.
- Sau khi quay phải, Node sibling sẽ lên làm cha. Do đó, về màu sắc, sib.right phải thay thế vai trò của sib. Và đương nhiên sib phải mang màu sắc của par.
- Par.color = BLACK. Vì Đên đôi (v) + Đỏ đơn(par) = Đen đơn(par)
Nhiều bạn sẽ thắc mắc rằng tại sao: mình ghi quay ở bước cuối nhưng trong hình lại quay ở bước đầu tiên? Thực ra thì bạn quay trước hay sau gì cũng được cả. Chỉ là do sau khi quay, vị trí các node có thay đổi nên mình đổi màu trước cho nó tiện.
b) Right left case – Phải trái
-
- Xảy ra: sib là con phải__ ngược lại trường hợp trên
- Xử lí:
-
-
- sib.left->color = par.color.
- par->color = BLACK
- rotateRight(sib)
- rotateLeft(par)
-
-
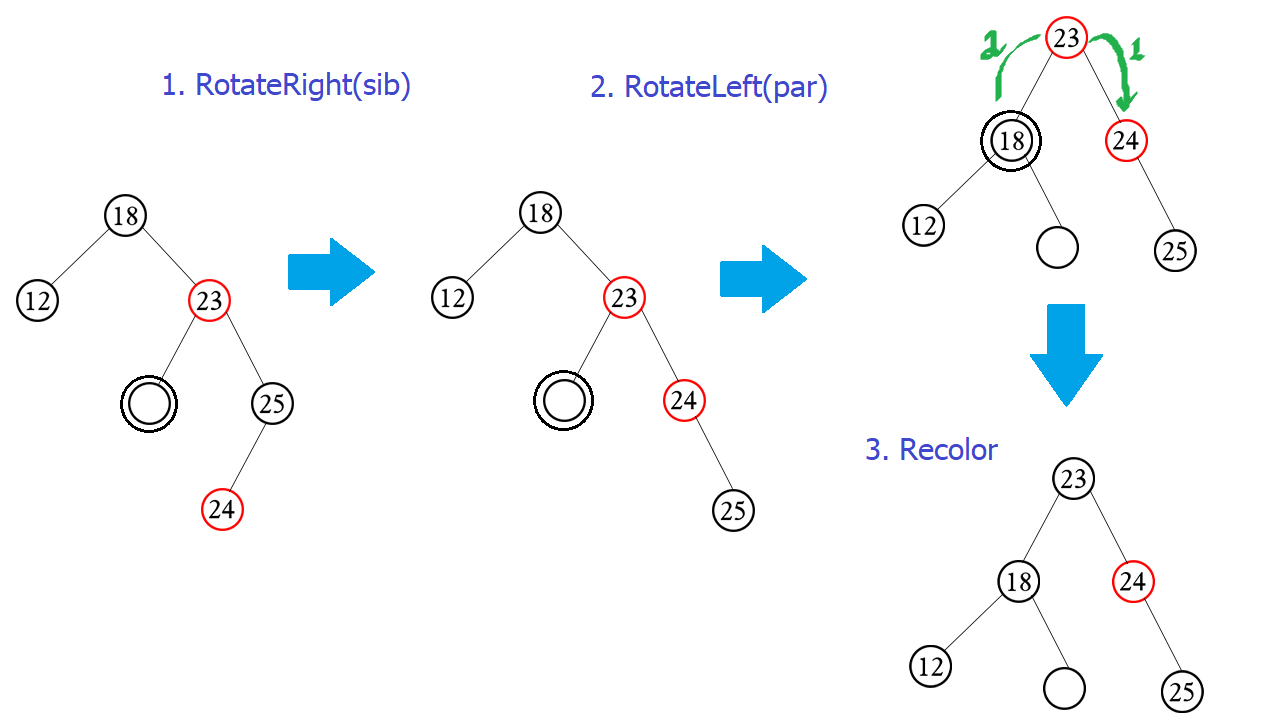
c) Left left case – Trái trái
-
- Xảy ra: sib là con trái__ sib.left->color == RED
- Xử lí:
-
-
- sib.left->color = sib.color.
- sib->color = sib.parent->color
- par->color = BLACK
- rotateRight(par)
-
-
d) Left right case – Trái phải
-
- Xảy ra: sib là con trái__ ngược lại trường hợp trên
- Xử lí:
-
-
- sib.right->color = par.color.
- par->color = BLACK
- rotateLeft(sib)
- rotateRight(par)
-
-
2. sibing.color == BLACK and NOT_hasRedChild(sibling)
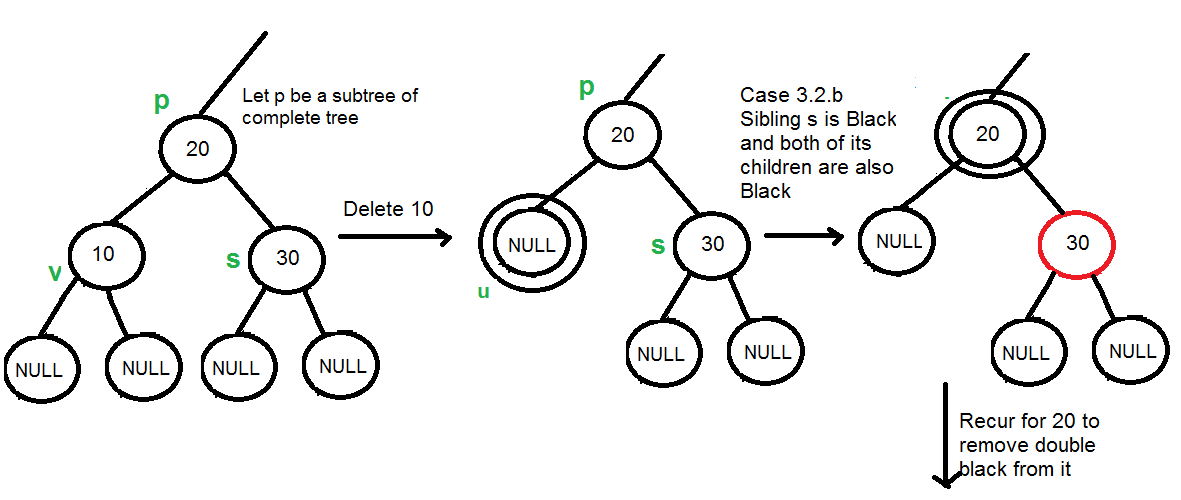
- Xử lí:
- sib.color = RED
- if par.color == BLACK
- fixDoubleBlack(par)
- else
- par.color = BLACK
- Có thể thấy Đen đôi (Double Black) tượng trưng cho việc thiếu hụt Node đen. Trong khi đó, Node Sibling có cả nhà màu đen (Node par auto đen nhé, nếu đỏ thì quy về u or v đỏ rồi). Vì vậy khi đổi sib.color = RED thì sẽ không gây ra xung đột đỏ.
- Và vì sao phải fixDoubleBlack(par)? Mình có thể giải thích nhưng nó sẽ dài. Các bạn tự suy nghĩ nhé :))) Gợi ý: Không thể có 3 Node đen tiếp (Bài 1 – Introduction)
3. sibing.color == 1 (RED)
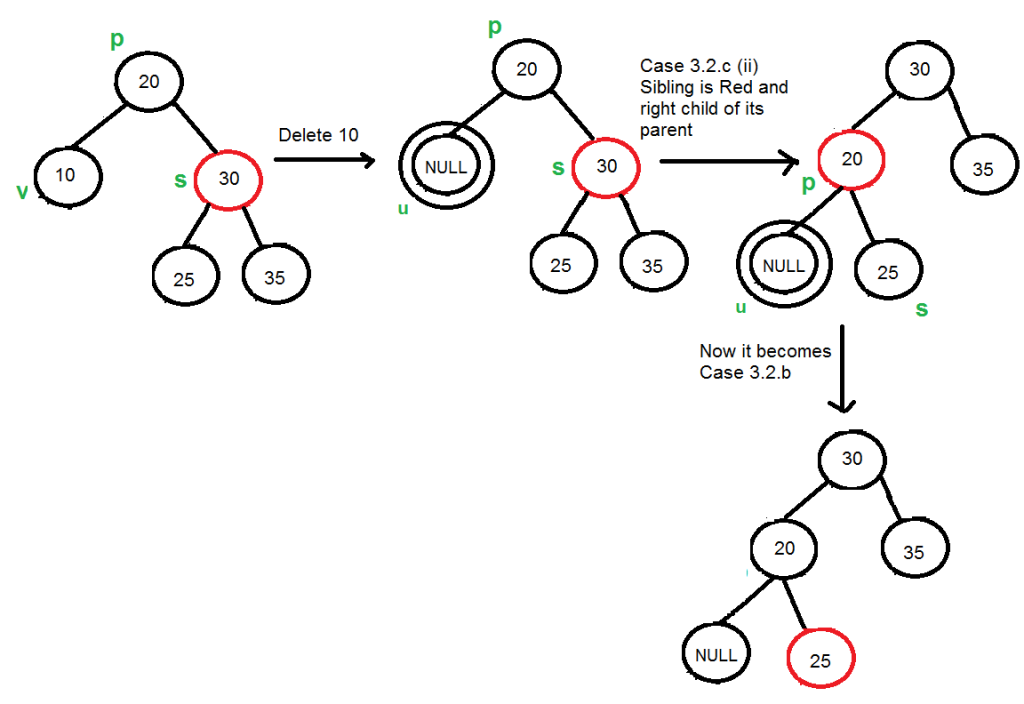
- Xử lí khá đơn giản. Nếu sib nằm bên phải thì quay trái cha – rotatLeft(par). Ngược lại thì quay trái – rotateLeft(par). Rồi sau đó tô lại màu – recolor.
- Như vậy ta đã đưa về TH – sibing.color == BLACK and hasRedChild(sibling). Giờ chỉ việc dùng lại hàm fixDoubleBlack cho Node u thôi.
|
1 2 3 4 5 6 7 8 9 10 |
if (sib->color == 1) { par->color = 1; sib->color = 0; if (sib->parent->left == sib) par = rotateRight(par); else par = rotateLeft(par); fixDoubleBlack(u); |
4. sibing == NULL
Coi vai trò DoubleBlack của u sang cho Node cha. Rồi FixDoubleBlack(par).
5. FixDoubleBlack() – CODE
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
void fixDoubleBlack(Node* root) { if (root == Root) return; Node* sib = sibling(root); Node* par = root->parent; if (sib == NULL) fixDoubleBlack(par); else { if (sib->color == 1) { par->color = 1; sib->color = 0; if (sib->parent->left == sib) par = rotateRight(par); else par = rotateLeft(par); fixDoubleBlack(root); } else { if (hasRedChild(sib)) { if (sib->parent->left == sib) { if (sib->left != NULL && sib->left->color) { sib->left->color = sib->color; sib->color = par->color; par->color = 0; par = rotateRight(par); } else { sib->right->color = par->color; par->color = 0; sib = rotateLeft(sib); par = rotateRight(par); } } else { if (sib->right != NULL && sib->right->color) { sib->right->color = sib->color; sib->color = par->color; par->color = 0; par = rotateLeft(par); } else { sib->left->color = par->color; par->color = 0; sib = rotateRight(sib); par = rotateLeft(par); } } } else { sib->color = 1; if (par->color == 0) fixDoubleBlack(par); else par->color = 0; } } } } |
4. Tiến hành xóa – deleteNode(Node* vDelete)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
void deleteNode(Node* vDelete) { Node* uReplace; if ((vDelete->left != NULL) && (vDelete->right != NULL)) uReplace = maxValueNode(vDelete->left); else if (vDelete->left != NULL) uReplace = vDelete->left; else if (vDelete->right != NULL) uReplace = vDelete->right; else uReplace = NULL; bool uvBlack = ((uReplace == NULL) || (uReplace->color == 0)) && (vDelete->color == 0); Node* par = vDelete->parent; Node* sib = sibling(vDelete); if (uReplace == NULL) { if (vDelete == Root) { Root = NULL; } else { if (uvBlack) fixDoubleBlack(vDelete); else if(sib != NULL) sib->color = 1; if (vDelete->parent->left == vDelete) par->left = NULL; else par->right = NULL; } delete vDelete; return; } if (vDelete->left == NULL || vDelete->right == NULL) { if (vDelete == Root) { vDelete->data = uReplace->data; vDelete->left = vDelete->right = NULL; delete uReplace; } else { if (vDelete->parent->left == vDelete) par->left = uReplace; else par->right = uReplace; delete vDelete; uReplace->parent = par; if (uvBlack) fixDoubleBlack(uReplace); else uReplace->color = 0; } return; } swapValues(uReplace, vDelete); deleteNode(uReplace); } |
5. Tổng kết – xóa ở cây đỏ đen
Full Code:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 |
#include <iostream> #include <cmath> using namespace std; #define COUNT 10 struct Node { int data; Node* left; Node* right; Node* parent; bool color; //1 -> Red | 0 -> Black }; Node* maxValueNode(Node* root) { Node* current = root; // Tìm kiếm Node có giá trị lớn nhất while (current->right != NULL) current = current->right; return current; } Node* sibling(Node* current) { if (current->parent == NULL) return NULL; if (current->parent->left == current) return current->parent->right; return current->parent->left; } void swapColors(Node* x1, Node* x2) { bool temp; temp = x1->color; x1->color = x2->color; x2->color = temp; } void swapValues(Node* u, Node* v) { int temp; temp = u->data; u->data = v->data; v->data = temp; } bool hasRedChild(Node* x) { if (x->right != NULL) if (x->right->color == 1) return true; if (x->left != NULL) if (x->left->color == 1) return true; return false; } string getColor(Node* root) { if (root->color == 1) return "RED"; return "BLACK"; } // In - Print 2D ra console void print2DUtil(Node* root, int space) { if (root == NULL) return; space += COUNT; print2DUtil(root->right, space); cout << endl; for (int i = COUNT; i < space; i++) cout << " "; cout << root->data << " (" << getColor(root) << ") " << "\n"; print2DUtil(root->left, space); } void print2D(Node* root) { print2DUtil(root, 0); } struct RedBlackTree { Node* Root; bool ll = false; bool rr = false; bool lr = false; bool rl = false; RedBlackTree() { Root = NULL; } Node* rotateRight(Node* root) { Node* x = root->left; // Gán x->right vào left root root->left = x->right; if (x->right != NULL) x->right->parent = root; x->parent = root->parent; if (root->parent == NULL) Root = x; else if (root->parent->left == root) root->parent->left = x; else root->parent->right = x; // Gán root vào x.right x->right = root; root->parent = x; // Trả về x return x; } Node* rotateLeft(Node* root) { Node* y = root->right; // Gán y->left vào right root root->right = y->left; if (y->left != NULL) y->left->parent = root; y->parent = root->parent; if (root->parent == NULL) Root = y; else if (root->parent->left == root) root->parent->left = y; else root->parent->right = y; // Gán root vào y.left y->left = root; root->parent = y; // Trả về y; return y; } Node* insertHelp(Node* root, int key) { // f đúng khi có xung đột RED RED bool f = false; if (root == NULL) { return new Node{ key, NULL, NULL, NULL, 1 }; // RED Node } else if (key < root->data) { root->left = insertHelp(root->left, key); root->left->parent = root; // root->left = Node X // root = X->parent if (Root != root) { if (root->color == root->left->color == 1) f = true; } } else { root->right = insertHelp(root->right, key); root->right->parent = root; // root->right = Node X // root = X->parent if (Root != root) { if (root->color == root->right->color == 1) f = true; } } // Xử lý 4 TH lệch // *** Khi này (ll, lr, rr, rl = false) nên chưa xử lí liền // *** Sau khi thoát 1 vòng đệ quy thì: root = X->parent->parent // *** Tức là Node ông, lúc này ta quay Node ông // Case 1 : Left left - Trái trái if (ll) { root = rotateRight(root); root->color = 0; root->right->color = 1; ll = false; } // Case 2 : Right right - Phải phải else if (rr) { root = rotateLeft(root); root->color = 0; root->left->color = 1; rr = false; } // Case 3 : Left right - Phải trái else if (lr) { root->left = rotateLeft(root->left); root->left->parent = root; root = rotateRight(root); root->color = 0; root->right->color = 1; lr = false; } // Case 4 : Right left - Phải trái else if (rl) { root->right = rotateRight(root->right); root->right->parent = root; root = rotateLeft(root); root->color = 0; root->left->color = 1; rl = false; } // Xử lí xung đột đỏ - RED RED if (f) { if (root->parent->right == root) { if (root->parent->left == NULL || root->parent->left->color == 0) { // Cha đỏ - chú đen (rr or rl) if (root->left != NULL && root->left->color == 1) rl = true; if (root->right != NULL && root->right->color == 1) rr = true; } else { // Cha đỏ - chú đỏ root->color = root->parent->left->color = 0; if (root != Root) root->parent->color = 1; } } else { if (root->parent->right == NULL || root->parent->right->color == 0) { // Cha đỏ - chú đen (ll or lr) if (root->left != NULL && root->left->color == 1) ll = true; if (root->right != NULL && root->right->color == 1) lr = true; } else { // Cha đỏ - chú đỏ root->color = root->parent->right->color = 0; if (root != Root) root->parent->color = 1; } } f = false; } return root; } void Insert(int key) { if (Root == NULL) { Root = new Node{ key, NULL, NULL, NULL, 0 }; } else { Root = insertHelp(Root, key); if (Root->color == 1) Root->color = 0; } } void fixDoubleBlack(Node* root) { if (root == Root) return; Node* sib = sibling(root); Node* par = root->parent; if (sib == NULL) fixDoubleBlack(par); else { if (sib->color == 1) { par->color = 1; sib->color = 0; if (sib->parent->left == sib) par = rotateRight(par); else par = rotateLeft(par); fixDoubleBlack(root); } else { if (hasRedChild(sib)) { if (sib->parent->left == sib) { if (sib->left != NULL && sib->left->color) { sib->left->color = sib->color; sib->color = par->color; par->color = 0; par = rotateRight(par); } else { sib->right->color = par->color; par->color = 0; sib = rotateLeft(sib); par = rotateRight(par); } } else { if (sib->right != NULL && sib->right->color) { sib->right->color = sib->color; sib->color = par->color; par->color = 0; par = rotateLeft(par); } else { sib->left->color = par->color; par->color = 0; sib = rotateRight(sib); par = rotateLeft(par); } } } else { sib->color = 1; if (par->color == 0) fixDoubleBlack(par); else par->color = 0; } } } } void deleteNode(Node* vDelete) { Node* uReplace; if ((vDelete->left != NULL) && (vDelete->right != NULL)) uReplace = maxValueNode(vDelete->left); else if (vDelete->left != NULL) uReplace = vDelete->left; else if (vDelete->right != NULL) uReplace = vDelete->right; else uReplace = NULL; bool uvBlack = ((uReplace == NULL) || (uReplace->color == 0)) && (vDelete->color == 0); Node* par = vDelete->parent; Node* sib = sibling(vDelete); if (uReplace == NULL) { if (vDelete == Root) { Root = NULL; } else { if (uvBlack) fixDoubleBlack(vDelete); else if(sib != NULL) sib->color = 1; if (vDelete->parent->left == vDelete) par->left = NULL; else par->right = NULL; } delete vDelete; return; } if (vDelete->left == NULL || vDelete->right == NULL) { if (vDelete == Root) { vDelete->data = uReplace->data; vDelete->left = vDelete->right = NULL; delete uReplace; } else { if (vDelete->parent->left == vDelete) par->left = uReplace; else par->right = uReplace; delete vDelete; uReplace->parent = par; if (uvBlack) fixDoubleBlack(uReplace); else uReplace->color = 0; } return; } swapValues(uReplace, vDelete); deleteNode(uReplace); } Node* search(int val) { Node* temp = Root; while (temp != NULL) { if (val < temp->data) { if (temp->left == NULL) return NULL; else temp = temp->left; } else if (val == temp->data) { break; } else { if (temp->right == NULL) return NULL; else temp = temp->right; } } return temp; } void Delete(int val) { Node* vDelete = search(val); if (vDelete == NULL) { cout << "\n ** Khong tim thay Node can xoa **\n"; return; } else { deleteNode(vDelete); } return; } }; int main() { RedBlackTree RBTree; RBTree.Insert(1); RBTree.Insert(4); RBTree.Insert(6); RBTree.Insert(3); RBTree.Insert(5); RBTree.Insert(7); RBTree.Insert(8); RBTree.Insert(2); RBTree.Insert(9); print2D(RBTree.Root); cout << "\n---------------------------\n"; RBTree.Delete(5); print2D(RBTree.Root); return 0; } |
Console:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
9 (RED) 8 (BLACK) 7 (RED) 6 (RED) 5 (BLACK) 4 (BLACK) 3 (RED) 2 (BLACK) 1 (RED) --------------------------- 9 (BLACK) 8 (RED) 7 (RED) 6 (BLACK) 4 (BLACK) 3 (RED) 2 (BLACK) 1 (RED) |
Chúc mừng bạn đã quay trúng ô “hại não”. Đọc hết đống này chắc các bạn đau đầu lắm :))) Mình định giải thích thêm nhưng bài đã dài lắm rồi. Nếu các bạn có thắc mắc gì thì có thể lên group Lập Trình Không Khó hỏi nhé. Ở đó, anh Nguyễn Văn Hiếu sẽ trực tiếp trả lời câu hỏi của bạn. Cảm ơn các rất nhiềuuuuuuuuuu.
Nguồn tham khảo: