Sàng nguyên tố - Code thuật toán sàng nguyên tố C++ và Java

Sàng nguyên tố Eratosthenes là một thuật toán giúp bạn nhanh chóng liệt kê các số nguyên tố. Đây là một thuật toán tìm số nguyên tố tối ưu khi muốn tìm tất cả các số nguyên tố nhỏ hơn một số N cho trước (N >=2). Vì đơn giản là số nguyên tố nhỏ nhất là 2 mà.

Định nghĩa số nguyên tố

Số nguyên tố là số nguyên dương có duy nhất 2 ước phân biệt là 1 và chính nó. Số nguyên tố nhỏ nhất là số 2.

Nếu bạn muốn kiểm tra một số có phải số nguyên tố hay không, hãy đọc bài thuật toán kiểm tra số nguyên tố

Nội dung trình bày:

Ý tưởng của thuật toán sàng nguyên tố Eratosthenes
Thuật toán
Triển khai thuật toán sử dụng C/C++, Java

Ý tưởng của thuật toán sàng nguyên tố Eratosthenes

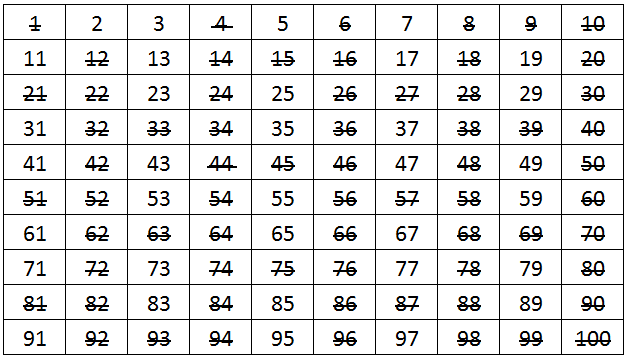
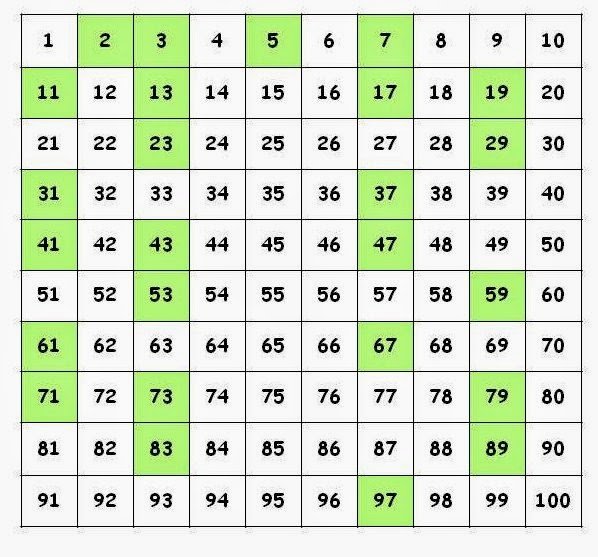
Dựa theo lý thuyết về số nguyên tố: Một số nguyên tố là số chỉ có 2 ước là 1 và chính nó. Do vậy, nếu ta xác định được số x là số nguyên tố, ta có thể kết luận mọi số chia hết cho x đều không phải số nguyên tố. Do đó ta đã loại bỏ được rất nhiều số mà không cần kiểm tra.

Ví dụ:

Số 2 là số nguyên tố => các số 4, 6, 8, 10, ... không phải số nguyên tố.

Số 3 là số nguyên tố => các số 9, 15, 21, ... không phải số nguyên tố. (Do 6, 12, 18 đã bị loại ở số 2)

Thuật toán sàng nguyên tố Eratosthenes

Tạo mảng đánh dấu cho tất cả các phần tử từ 2 đến N và mặc định tất cả đều là số nguyên tố
Xét số đầu tiên tìm được là số nguyên tố – giả sử x, đánh dấu tất cả các ước của x: 2x, 3x, 4x,… trong đoạn [x, N] không phải số nguyên tố.
Tìm số tiếp theo được đánh dấu là số nguyên tố trong [x, N]. Nếu không còn số nào, thoát chương trình. Nếu còn, gán nó bằng x và lặp lại bước 2.
Khi kết thúc giải thuật, các số không bị đánh dấu là các số nguyên tố

Cài đặt thuật toán sàng nguyên tố

Ngôn ngữ C/C++

// Code from https://blog.luyencode.net

#include <stdio.h>

int main() {
  int N = 1000;
  bool check[N + 1];
  // Khởi tạo tất cả các số [2...N] đều là số nguyên tố
  for (int i = 2; i <= N; i++) {
    check[i] = true;
  }

  // Thuật toán sàng nguyên tố
  // Nếu một số là số nguyên tố, thì tất cả các bội của nó không phải số nguyên tố
  for (int i = 2; i <= N; i++) {
    if (check[i] == true) {
      for (int j = 2 * i; j <= N; j += i) {
        check[j] = false;
      }
    }
  }
  // In ra các số là số nguyên tố
  for (int i = 2; i <= N; i++) {
    if (check[i] == true) {
      printf("%d ", i);
    }
  }
}

// Code from https://blog.luyencode.net

#include <stdio.h>

int main() {

int N = 1000;

bool check[N + 1];

// Khởi tạo tất cả các số [2...N] đều là số nguyên tố

for (int i = 2; i <= N; i++) {

check[i] = true;

}

// Thuật toán sàng nguyên tố

// Nếu một số là số nguyên tố, thì tất cả các bội của nó không phải số nguyên tố

for (int i = 2; i <= N; i++) {

if (check[i] == true) {

for (int j = 2 * i; j <= N; j += i) {

check[j] = false;

}

// In ra các số là số nguyên tố

for (int i = 2; i <= N; i++) {

if (check[i] == true) {

printf("%d ", i);

}

Cài đặt sử dụng Java

// Code from https://blog.luyencode.net

import java.util.*;
import java.lang.*;
import java.io.*;

/* Name of the class has to be "Main" only if the class is public. */
class Eratosthenes {
  public static void main (String[] args) throws java.lang.Exception {
    int N = 1000;
    boolean[] check = new boolean[N + 1];
    // Khởi tạo tất cả các số [2...N] đều là số nguyên tố
    for (int i = 2; i <= N; i++) {
      check[i] = true;
    }

    // Thuật toán sàng nguyên tố
    // Nếu một số là số nguyên tố, thì tất cả các bội của nó không phải số nguyên tố
    for (int i = 2; i <= N; i++) {
      if (check[i] == true) {
        for (int j = 2 * i; j <= N; j += i) {
          check[j] = false;
        }
      }
    }
    // In ra các số là số nguyên tố
    for (int i = 2; i <= N; i++) {
      if (check[i] == true) {
        System.out.print(i + " ");
      }
    }
  }
}

// Code from https://blog.luyencode.net

import java.util.*;

import java.lang.*;

import java.io.*;

/* Name of the class has to be "Main" only if the class is public. */

class Eratosthenes {

public static void main (String[] args) throws java.lang.Exception {

int N = 1000;

boolean[] check = new boolean[N + 1];

// Khởi tạo tất cả các số [2...N] đều là số nguyên tố

for (int i = 2; i <= N; i++) {

check[i] = true;

}

// Thuật toán sàng nguyên tố

// Nếu một số là số nguyên tố, thì tất cả các bội của nó không phải số nguyên tố

for (int i = 2; i <= N; i++) {

if (check[i] == true) {

for (int j = 2 * i; j <= N; j += i) {

check[j] = false;

}

// In ra các số là số nguyên tố

for (int i = 2; i <= N; i++) {

if (check[i] == true) {

System.out.print(i + " ");

}

Kết quả khi chạy:

2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997

2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997